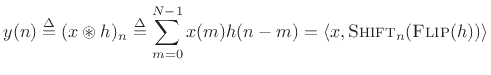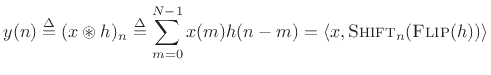Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As mentioned above, cyclic convolution can be written as
where
 and
and
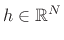 . It is instructive to interpret this
expression graphically, as depicted in Fig.7.5 above. The
convolution result at time
. It is instructive to interpret this
expression graphically, as depicted in Fig.7.5 above. The
convolution result at time 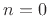 is the inner product of
is the inner product of 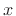 and
and
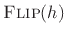 , or
, or
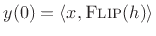 . For the next time instant,
. For the next time instant,
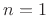 , we shift
, we shift
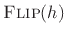 one sample to the right and repeat the
inner product operation to obtain
one sample to the right and repeat the
inner product operation to obtain
 ,
and so on. To capture the cyclic nature of the convolution,
,
and so on. To capture the cyclic nature of the convolution, 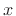 and
and
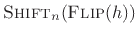 can be imagined plotted on a cylinder.
Thus, Fig.7.5 shows the cylinder after being ``cut'' along the
vertical line between
can be imagined plotted on a cylinder.
Thus, Fig.7.5 shows the cylinder after being ``cut'' along the
vertical line between  and
and 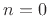 and ``unrolled'' to lay flat.
and ``unrolled'' to lay flat.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]