Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 7.5:
Illustration of convolution of
![$ y=[1,1,1,1,0,0,0,0]$](img45.png) and ``matched filter''
and ``matched filter''
![$ h=\protect\hbox{\sc Flip}(y)=[1,0,0,0,0,1,1,1]$](img1177.png) (
( ).
).
![\includegraphics[width=2.5in]{eps/conv}](img1178.png) |
Figure 7.5 illustrates convolution of
to get
![$\displaystyle y\circledast h = [4,3,2,1,0,1,2,3]. \protect$](img1180.png) |
(7.3) |
For example,  could be a ``rectangularly windowed signal, zero-padded by
a factor of 2,'' where the signal happened to be dc (all
could be a ``rectangularly windowed signal, zero-padded by
a factor of 2,'' where the signal happened to be dc (all 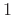 s).
For the
convolution, we need
s).
For the
convolution, we need
which is the same as  . When
. When
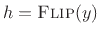 , we say that
, we say that  is a
matched filter for
is a
matched filter for  .7.7 In this case,
.7.7 In this case, 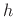 is matched to look for a
``dc component,'' and also zero-padded by a factor of
is matched to look for a
``dc component,'' and also zero-padded by a factor of 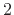 . The
zero-padding serves to simulate acyclic convolution using circular
convolution. Note from Eq.(7.3) that the maximum is obtained
in the convolution output at time 0
. This peak (the largest
possible if all input signals are limited to
. The
zero-padding serves to simulate acyclic convolution using circular
convolution. Note from Eq.(7.3) that the maximum is obtained
in the convolution output at time 0
. This peak (the largest
possible if all input signals are limited to ![$ [-1,1]$](img1183.png) in magnitude),
indicates the matched filter has ``found'' the dc signal starting at
time 0
. This peak would persist in the presence of some amount of
noise and/or interference from other signals. Thus, matched filtering
is useful for detecting known signals in the presence of noise and/or
interference [35].
in magnitude),
indicates the matched filter has ``found'' the dc signal starting at
time 0
. This peak would persist in the presence of some amount of
noise and/or interference from other signals. Thus, matched filtering
is useful for detecting known signals in the presence of noise and/or
interference [35].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=2.5in]{eps/conv}](img1178.png)
![\begin{eqnarray*}
y&=&[1,1,1,1,0,0,0,0] \\
h&=&[1,0,0,0,0,1,1,1]
\end{eqnarray*}](img1179.png)