Definition: The circular cross-correlation of two signals
Definition: The circular cross-correlation of two signals ![]() and
and
![]() in
in
![]() may be defined by
may be defined by

(Note that the ``lag''
The term ``cross-correlation'' comes from
statistics, and what we have defined here is more properly
called a ``sample cross-correlation.''
That is,
![]() is an
estimator8.8 of the true
cross-correlation
is an
estimator8.8 of the true
cross-correlation ![]() which is an assumed statistical property
of the signal itself. This definition of a sample cross-correlation is only valid for
stationary stochastic processes, e.g., ``steady noises'' that
sound unchanged over time. The statistics of a stationary stochastic
process are by definition time invariant, thereby allowing
time-averages to be used for estimating statistics such
as cross-correlations. For brevity below, we will typically
not include the ``sample'' qualifier, because all computational
methods discussed will be sample-based methods intended for use on
stationary data segments.
which is an assumed statistical property
of the signal itself. This definition of a sample cross-correlation is only valid for
stationary stochastic processes, e.g., ``steady noises'' that
sound unchanged over time. The statistics of a stationary stochastic
process are by definition time invariant, thereby allowing
time-averages to be used for estimating statistics such
as cross-correlations. For brevity below, we will typically
not include the ``sample'' qualifier, because all computational
methods discussed will be sample-based methods intended for use on
stationary data segments.
The DFT of the cross-correlation may be called the cross-spectral density, or ``cross-power spectrum,'' or even simply ``cross-spectrum'':
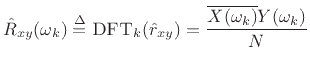
The last equality above follows from the correlation theorem (§7.4.7).