Unbiased Cross-Correlation

Recall that the cross-correlation operator is cyclic (circular) since $n+l$ is interpreted modulo $N$ . In practice, we are normally interested in estimating the acyclic cross-correlation between two signals. For this (more realistic) case, we may define instead the unbiased cross-correlation

$$\zbox {{\hat r}^u_{xy}(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} y(n+l),\quad l = 0,1,2,\ldots,L-1}$$

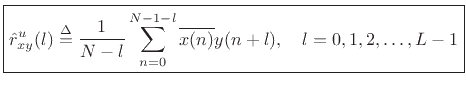
where we choose $L\ll N$ (e.g., $L\approx\sqrt{N}$ ) in order to have enough lagged products $\overline{x(n)} y(n+l)$ at the highest lag $L-1$ so that a reasonably accurate average is obtained. Note that the summation stops at $n=N-l-1$ to avoid cyclic wrap-around of $n$ modulo $N$ . The term ``unbiased'' refers to the fact that the expected value^8.9[34] of ${\hat r}^u_{xy}(l)$ is the true cross-correlation $r_{xy}(l)$ of $x$ and $y$ (assumed to be samples from stationary stochastic processes).

An unbiased acyclic cross-correlation may be computed faster via DFT (FFT) methods using zero padding:

$$\zbox {{\hat r}^u_{xy}(l) = \frac{1}{N-l}\hbox{\sc IDFT}_l(\overline{X}\cdot Y), \quad l = 0,1,2,\ldots,L-1}$$

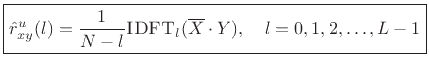
where

$$\begin{eqnarray*} X &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(x)]\\ Y &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(y)]. \end{eqnarray*}$$

Note that $x$ and $y$ belong to $\mathbb{C}^N$ while $X$ and $Y$ belong to $\mathbb{C}^{N+L-1}$ . The zero-padding may be causal (as defined in §7.2.8) because the signals are assumed to be be stationary, in which case all signal statistics are time-invariant. As usual when embedding acyclic correlation (or convolution) within the cyclic variant given by the DFT, sufficient zero-padding is provided so that only zeros are ``time aliased'' (wrapped around in time) by modulo indexing.

Cross-correlation is used extensively in audio signal processing for applications such as time scale modification, pitch shifting, click removal, and many others.