Autocorrelation

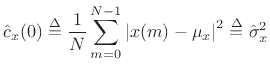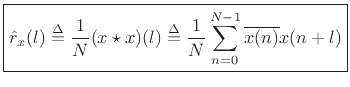
The cross-correlation of a signal with itself gives its autocorrelation:

$$\zbox {{\hat r}_x(l) \isdef \frac{1}{N}(x\star x)(l) \isdef \frac{1}{N}\sum_{n=0}^{N-1}\overline{x(n)} x(n+l)}$$

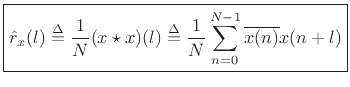
The autocorrelation function is Hermitian:

$${\hat r}_x(-l) = \overline{{\hat r}_x(l)}$$

When $x$ is real, its autocorrelation is real and even (symmetric about lag zero).

The unbiased cross-correlation similarly reduces to an unbiased autocorrelation when $x\equiv y$:

$$\zbox {{\hat r}^u_x(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} x(n+l),\quad l = 0,1,2,\ldots,L-1} \protect$$ (8.2)

The DFT of the true autocorrelation function $r_x(n)\in{\bf R}^N$ is the (sampled) power spectral density (PSD), or power spectrum, and may be denoted

$$R_x(\omega_k) \isdef \hbox{\sc DFT}_k(r_x).$$

The complete (not sampled) PSD is $R_x(\omega) \isdef \hbox{\sc DTFT}_k(r_x)$, where the DTFT is defined in Appendix B (it's just an infinitely long DFT). The DFT of ${\hat r}_x$ thus provides a sample-based estimate of the PSD:^8.7

$${\hat R}_x(\omega_k)=\hbox{\sc DFT}_k({\hat r}_x) = \frac{\left\vert X(\omega_k)\right\vert^2}{N}$$

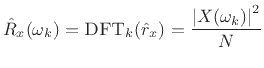
We could call ${\hat R}_x(\omega_k)$ a ``sampled sample power spectral density''.

At lag zero, the autocorrelation function reduces to the average power (mean square) which we defined in §5.8:

$${\hat r}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)\right\vert^2 % \isdef \Pscr_x^2$$

Replacing ``correlation'' with ``covariance'' in the above definitions gives corresponding zero-mean versions. For example, we may define the sample circular cross-covariance as

$$\zbox {{\hat c}_{xy}(n) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\overline{[x(m)-\mu_x]} [y(m+n)-\mu_y].}$$

where $\mu_x$ and $\mu_y$ denote the means of $x$ and $y$, respectively. We also have that ${\hat c}_x(0)$ equals the sample variance of the signal $x$:

$${\hat c}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)-\mu_x\right\vert^2 \isdef {\hat \sigma}_x^2$$