If we add enough trailing zeros to the signals being convolved, we can
obtain acyclic convolution embedded within a cyclic
convolution. How many zeros do we need to add? Suppose the signal
![]() consists of
consists of ![]() contiguous nonzero samples at times 0
to
contiguous nonzero samples at times 0
to
![]() , preceded and followed by zeros, and suppose
, preceded and followed by zeros, and suppose ![]() is nonzero
only over a block of
is nonzero
only over a block of ![]() samples starting at time 0. Then the
acyclic convolution of
samples starting at time 0. Then the
acyclic convolution of ![]() with
with ![]() reduces to
reduces to
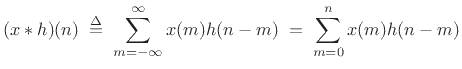 |
(9.15) |
The number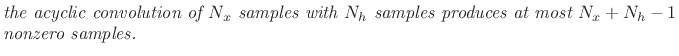
| (9.16) |
When ![]() or
or ![]() is infinity, the convolution result can be as
small as 1. For example, consider
is infinity, the convolution result can be as
small as 1. For example, consider
![]() , with
, with
![]() , and
, and
![]() . Then
. Then
![]() . This is an example of what is called deconvolution.
In the frequency domain, deconvolution always involves a pole-zero
cancellation. Therefore, it is only possible when
. This is an example of what is called deconvolution.
In the frequency domain, deconvolution always involves a pole-zero
cancellation. Therefore, it is only possible when ![]() or
or ![]() is
infinite. In practice, deconvolution can sometimes be accomplished
approximately, particularly within narrow frequency bands
[119].
is
infinite. In practice, deconvolution can sometimes be accomplished
approximately, particularly within narrow frequency bands
[119].
We thus conclude that, to embed acyclic convolution within a cyclic
convolution (as provided by an FFT), we need to zero-pad both
operands out to length ![]() , where
, where ![]() is at least the sum of the
operand lengths (minus one).
is at least the sum of the
operand lengths (minus one).