Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A class of causal, FIR, two-channel, critically sampled, exact
perfect-reconstruction filter-banks is the set of so-called
Conjugate Quadrature Filters (CQF). In the z-domain, the CQF
relationships are
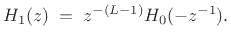 |
(12.39) |
In the time domain, the analysis and synthesis filters are given by
That is,
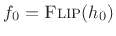 for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by
for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by  .
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter
.
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter 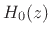 . It can be shown that this is an
orthogonal filter bank. The analysis filters
. It can be shown that this is an
orthogonal filter bank. The analysis filters 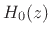 and
and
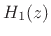 are power complementary, i.e.,
are power complementary, i.e.,
 |
(12.40) |
or
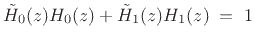 |
(12.41) |
where
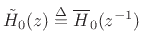 denotes the
paraconjugate of
denotes the
paraconjugate of 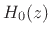 (for real filters
(for real filters 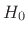 ). The
paraconjugate is the analytic continuation of
). The
paraconjugate is the analytic continuation of
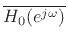 from
the unit circle to the
from
the unit circle to the 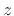 plane. Moreover, the analysis filters
plane. Moreover, the analysis filters
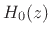 are power symmetric, e.g.,
are power symmetric, e.g.,
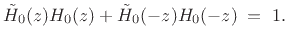 |
(12.42) |
The power symmetric case was introduced by Smith and Barnwell in 1984
[272].
With the CQF constraints, (11.18) reduces to
![$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[H_0(z)H_0(z^{-1}) + H_0(-z)H_0(-z^{-1})\right]X(z) \protect$](img2071.png) |
(12.43) |
Let
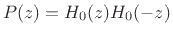 , such that
, such that 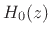 is a spectral factor of
the half-band filter
is a spectral factor of
the half-band filter 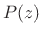 (i.e.,
(i.e., 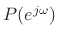 is a nonnegative power
response which is lowpass, cutting off near
is a nonnegative power
response which is lowpass, cutting off near
 ). Then,
(11.43) reduces to
). Then,
(11.43) reduces to
![$\displaystyle \hat{X}(z) \eqsp \frac{1}{2}\left[P(z) + P(-z)\right]X(z) \eqsp -z^{-(L-1)}X(z)$](img2076.png) |
(12.44) |
The problem of PR filter design has thus been reduced to designing
one half-band filter 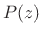 . It can be shown that any half-band
filter can be written in the form
. It can be shown that any half-band
filter can be written in the form
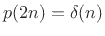 . That is, all
non-zero even-indexed values of
. That is, all
non-zero even-indexed values of  are set to zero.
are set to zero.
A simple design of an FIR half-band filter would be to window a sinc
function:
![$\displaystyle p(n) \eqsp \frac{\hbox{sin}[\pi n/2]}{\pi n/2}w(n)$](img2079.png) |
(12.45) |
where 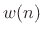 is any suitable window, such as the Kaiser window.
is any suitable window, such as the Kaiser window.
Note that as a result of (11.43), the CQF filters
are power complementary. That is, they satisfy
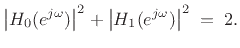 |
(12.46) |
Also note that the filters 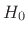 and
and 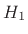 are not linear phase. It
can be shown that there are no two-channel perfect reconstruction
filter banks that have all three of the following characteristics
(except for the Haar filters):
are not linear phase. It
can be shown that there are no two-channel perfect reconstruction
filter banks that have all three of the following characteristics
(except for the Haar filters):
- FIR
- orthogonal
- linear phase
In this design procedure, we have chosen to satisfy the first two and
give up the third.
By relaxing ``orthogonality'' to ``biorthogonality'', it becomes
possible to obtain FIR linear phase filters in a critically sampled,
perfect reconstruction filter bank. (See §11.9.)
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\begin{eqnarray*}
h_1(n) &=& -(-1)^n h_0(L-1-n) \\ [5pt]
f_0(n) &=& h_0(L-1-n) \\ [5pt]
f_1(n) &=& -(-1)^n h_0(n) \eqsp - h_1(L-1-n).
\end{eqnarray*}](img2063.png)
![]() for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by
for the lowpass channel, and each highpass
channel filter is a modulation of its lowpass counterpart by ![]() .
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter
.
Again, all four analysis and synthesis filters are determined by the
lowpass analysis filter ![]() . It can be shown that this is an
orthogonal filter bank. The analysis filters
. It can be shown that this is an
orthogonal filter bank. The analysis filters ![]() and
and
![]() are power complementary, i.e.,
are power complementary, i.e.,
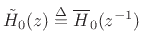 denotes the
paraconjugate of
denotes the
paraconjugate of ![]() , such that
, such that ![]() is a spectral factor of
the half-band filter
is a spectral factor of
the half-band filter ![]() (i.e.,
(i.e., ![]() is a nonnegative power
response which is lowpass, cutting off near
is a nonnegative power
response which is lowpass, cutting off near
![]() ). Then,
(11.43) reduces to
). Then,
(11.43) reduces to
![$\displaystyle p(n) \eqsp \frac{\hbox{sin}[\pi n/2]}{\pi n/2}w(n)$](img2079.png)