Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure 11.15 shows a simple two-channel band-splitting filter bank,
followed by the corresponding synthesis filter bank which
reconstructs the original signal (we hope) from the two channels. The
analysis filter 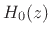 is a half-band lowpass filter, and
is a half-band lowpass filter, and 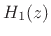 is a complementary half-band highpass filter. The synthesis filters
is a complementary half-band highpass filter. The synthesis filters
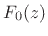 and
and 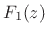 are to be derived. Intuitively, we expect
are to be derived. Intuitively, we expect
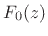 to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and
to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and 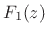 should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
![\begin{psfrags}
% latex2html id marker 30377\psfrag{x(n)}{\normalsize $x(n)$}\psfrag{x}{\normalsize $x$}\psfrag{(n)}{\normalsize $(n)$}\psfrag{y}{\normalsize $y$}\psfrag{v}{\normalsize $v$}\psfrag{H}{\normalsize $H$}\psfrag{F}{\normalsize $F$}\psfrag{z}{\normalsize $z$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/cqf}
\caption{Two-channel critically sampled filter bank.}
\end{figure}
\end{psfrags}](img1978.png)
The outputs of the two analysis filters in Fig.11.15 are
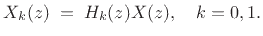 |
(12.16) |
Using the results of §11.1, the signals become, after
downsampling,
![$\displaystyle V_k(z) \eqsp \frac{1}{2}\left[X_k(z^{1/2}) + X_k(-z^{1/2})\right], \; k=0,1.$](img1980.png) |
(12.17) |
After upsampling, the signals become
After substitutions and rearranging, we find that the output  is a filtered replica of the input signal plus an aliasing term:
is a filtered replica of the input signal plus an aliasing term:
For perfect reconstruction, we require the aliasing term to be
zero. For ideal half-band filters cutting off at
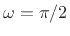 , we
can choose
, we
can choose 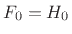 and
and 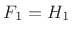 and the aliasing term is zero
because there is no spectral overlap between the channels, i.e.,
and the aliasing term is zero
because there is no spectral overlap between the channels, i.e.,
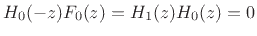 , and
, and
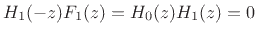 .
However, more generally (and more practically), we can force the
aliasing to zero by choosing synthesis filters
.
However, more generally (and more practically), we can force the
aliasing to zero by choosing synthesis filters
In this case, synthesis filter 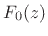 is still a lowpass, but the
particular one obtained by
is still a lowpass, but the
particular one obtained by  -rotating the highpass analysis
filter around the unit circle in the
-rotating the highpass analysis
filter around the unit circle in the 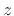 plane. Similarly, synthesis
filter
plane. Similarly, synthesis
filter 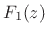 is the
is the  -rotation (and negation) of the analysis
lowpass filter
-rotation (and negation) of the analysis
lowpass filter 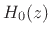 on the unit circle.
For this choice of synthesis filters
on the unit circle.
For this choice of synthesis filters  and
and 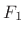 , aliasing is
completely canceled for any choice of analysis filters
, aliasing is
completely canceled for any choice of analysis filters 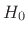 and
and 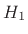 .
.
Referring again to (11.18), we see that we also need the
non-aliased term to be of the form
where  is of the form
is of the form
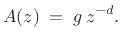 |
(12.21) |
That is, for perfect reconstruction, we need, in addition to aliasing
cancellation, that the non-aliasing term reduce to a constant gain 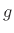 and/or delay
and/or delay 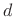 . We will call this the filtering cancellation
constraint on the channel filters. Thus perfect reconstruction
requires both aliasing cancellation and filtering cancellation.
. We will call this the filtering cancellation
constraint on the channel filters. Thus perfect reconstruction
requires both aliasing cancellation and filtering cancellation.
Let
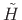 denote
denote 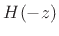 . Then both constraints can be expressed in
matrix form as follows:
. Then both constraints can be expressed in
matrix form as follows:
![$\displaystyle \left[\begin{array}{cc} H_0 & H_1 \\ [2pt] {\tilde H}_0 & {\tilde H}_1 \end{array}\right]\left[\begin{array}{c} F_0 \\ [2pt] F_1 \end{array}\right]\eqsp \left[\begin{array}{c} c \\ [2pt] 0 \end{array}\right]$](img2005.png) |
(12.22) |
Substituting the aliasing-canceling choices for  and
and 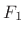 from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain
from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain
The filtering-cancellation constraint is almost satisfied by ideal
zero-phase half-band filters cutting off at 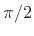 , since in that
case we have
, since in that
case we have
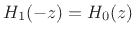 and
and
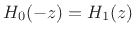 . However, the
minus sign in (11.23) means there is a discontinuous sign flip as
frequency crosses
. However, the
minus sign in (11.23) means there is a discontinuous sign flip as
frequency crosses
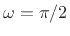 , which is not equivalent to a linear
phase term. Therefore the filtering cancellation constraint fails for
the ideal half-band filter bank! Recall from above, however, that
ideal half-band filters did work using a different choice of
synthesis filters, relying instead on their lack of spectral overlap.
The presently studied case from (11.19) arose from so-called
Quadrature Mirror Filters (QMF), which are discussed further
below. First, however, we'll look at some simple special cases.
, which is not equivalent to a linear
phase term. Therefore the filtering cancellation constraint fails for
the ideal half-band filter bank! Recall from above, however, that
ideal half-band filters did work using a different choice of
synthesis filters, relying instead on their lack of spectral overlap.
The presently studied case from (11.19) arose from so-called
Quadrature Mirror Filters (QMF), which are discussed further
below. First, however, we'll look at some simple special cases.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is a half-band lowpass filter, and
is a half-band lowpass filter, and ![]() is a complementary half-band highpass filter. The synthesis filters
is a complementary half-band highpass filter. The synthesis filters
![]() and
and ![]() are to be derived. Intuitively, we expect
are to be derived. Intuitively, we expect
![]() to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and
to be a lowpass that rejects the upper half-band due to the
upsampler by 2, and ![]() should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
should do the same but then also
reposition its output band as the upper half-band, which can be
accomplished by selecting the upper of the two spectral images in the
upsampler output.
![$\displaystyle V_k(z) \eqsp \frac{1}{2}\left[X_k(z^{1/2}) + X_k(-z^{1/2})\right], \; k=0,1.$](img1980.png)
![$\displaystyle \frac{1}{2}[X_k(z) + X_k(-z)]$](img1982.png)
![$\displaystyle \frac{1}{2}[H_k(z)X(z) + H_k(-z)X(-z)],\; k=0,1.$](img1983.png)
![]() denote
denote ![]() . Then both constraints can be expressed in
matrix form as follows:
. Then both constraints can be expressed in
matrix form as follows:
![$\displaystyle \left[\begin{array}{cc} H_0 & H_1 \\ [2pt] {\tilde H}_0 & {\tilde H}_1 \end{array}\right]\left[\begin{array}{c} F_0 \\ [2pt] F_1 \end{array}\right]\eqsp \left[\begin{array}{c} c \\ [2pt] 0 \end{array}\right]$](img2005.png)
![]() and
and ![]() from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain
from
(11.19) into the filtering-cancellation constraint (11.20), we
obtain