Conclusions

We can note the following points regarding our single-sideband FIR filter design by means of direct Fourier intuition, frequency-sampling, and the window-method:

• The pass-band ripple is much smaller than 0.1 dB, which is ``over designed'' and therefore wasting of taps.

• The stop-band response ``droops'' which ``wastes'' filter taps when stop-band attenuation is the only stop-band specification. In other words, the first stop-band ripple drives the spec (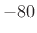$-80$ dB), while all higher-frequency ripples are over-designed. On the other hand, a high-frequency ``roll-off'' of this nature is quite natural in the frequency domain, and it corresponds to a ``smoother pulse'' in the time domain. Sometimes making the stop-band attenuation uniform will cause small impulses at the beginning and end of the impulse response in the time domain. (The pass-band and stop-band ripple can ``add up'' under the inverse Fourier transform integral.) Recall this impulsive endpoint phenomenon for the Chebyshev window shown in Fig.3.33.

• The pass-band is degraded by early roll-off. The pass-band edge is not exactly in the desired place.

• The filter length can be thousands of taps long without running into numerical failure. Filters this long are actually needed for sampling rate conversion [270,218].

We can also note some observations regarding the optimal Chebyshev version designed by the Remez multiple exchange algorithm:

• The stop-band is ideal, equiripple.

• The transition bandwidth is close to half that of the window method. (We already knew our chosen transition bandwidth was not ``tight'', but our rule-of-thumb based on the Kaiser-window main-lobe width predicted only about 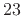$23$ % excess width.)

• The pass-band is ideal, though over-designed for static audio spectra.

• The computational design time is orders of magnitude larger than that for window method.

• The design fails to converge for filters much longer than 256 taps. (Need to increase working precision or use a different method to get longer optimal Chebyshev FIR filters.)

Practical application of Hilbert-transform filters to phase-vocoder analysis for additive synthesis is discussed in §G.10.