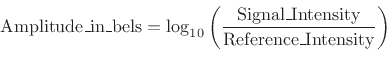
A decibel (abbreviated dB) is defined as one tenth of a bel. The belF.1 is an amplitude unit defined for sound as the log (base 10) of the intensity relative to some reference intensity,F.2 i.e.,
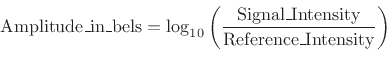
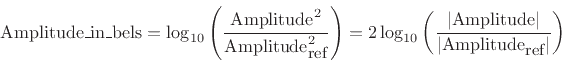
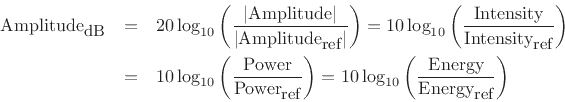
A just-noticeable difference (JND) in amplitude level is on the order of a quarter dB. In the early days of telephony, one dB was considered a reasonable ``smallest step'' in amplitude, but in reality, a series of half-dB amplitude steps does not sound very smooth, while quarter-dB steps do sound pretty smooth. A typical professional audio filter-design specification for ``ripple in the passband'' is 0.1 dB.