Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
By Euler's identity,
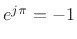 , so that
, so that
from which it follows that for any 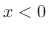 ,
,
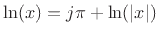 .
.
Similarly,
 , so that
, so that
and for any imaginary number 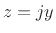 ,
,
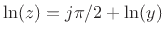 ,
where
,
where  is real.
is real.
Finally, from the polar representation
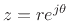 for
complex numbers,
for
complex numbers,
where  and
and 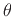 are real. Thus, the log of the magnitude of
a complex number behaves like the log of any positive real number,
while the log of its phase term
are real. Thus, the log of the magnitude of
a complex number behaves like the log of any positive real number,
while the log of its phase term
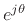 extracts its phase
(times
extracts its phase
(times  ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , so that
, so that
![]() , so that
, so that
![]() for
complex numbers,
for
complex numbers,