As mentioned in §G.7, the phase vocoder had become a standard analysis tool for additive synthesis (§G.8) by the late 1970s [186,187]. This section summarizes that usage.
In analysis for additive synthesis, we convert a time-domain signal
![]() into a collection of amplitude envelopes
into a collection of amplitude envelopes ![]() and frequency envelopes
and frequency envelopes
![]() (or phase modulation envelopes
(or phase modulation envelopes
![]() ), as graphed in Fig.G.12.
It is usually desired that these envelopes be slowly varying
relative to the original signal. This leads to the assumption that we
have at most one sinusoid in each filter-bank channel. (By
``sinusoid'' we mean, of course, ``quasi sinusoid,'' since its
amplitude and phase may be slowly time-varying.) The channel-filter
frequency response is given by the FFT of the analysis window used
(Chapter 9).
), as graphed in Fig.G.12.
It is usually desired that these envelopes be slowly varying
relative to the original signal. This leads to the assumption that we
have at most one sinusoid in each filter-bank channel. (By
``sinusoid'' we mean, of course, ``quasi sinusoid,'' since its
amplitude and phase may be slowly time-varying.) The channel-filter
frequency response is given by the FFT of the analysis window used
(Chapter 9).
The signal in the ![]() subband (filter-bank channel) can be
written
subband (filter-bank channel) can be
written
Typically, the instantaneous phase modulation ![]() is
differentiated to obtain instantaneous frequency deviation:
is
differentiated to obtain instantaneous frequency deviation:
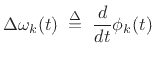 |
(G.4) |