Phasing with First-Order Allpass Filters

The block diagram of a typical inexpensive phase shifter for guitar players is shown in Fig.8.23.^9.20 It consists of a series chain of first-order allpass filters,^9.21 each having a single time-varying parameter $g_i(n)$ controlling the pole and zero location over time, plus a feedforward path through gain $g$ which is a fixed depth control. Thus, the delay line of the flanger is replaced by a string of allpass filters. (A delay line is of course an allpass filter itself.)

Figure 8.23: Structure of a phaser based on four first-order allpass filters.

In analog hardware, the first-order allpass transfer function [452, Appendix E, Section 8]^9.22is

$$\hbox{AP}_{1}^{\,\omega_b} \isdef \frac{s-\omega_b}{s+\omega_b}. \protect$$ (9.19)

(In classic phaser circuits such as the Univibe, $-\hbox{AP}_{1}^{\,\omega_b}$ is used, but since there is an even number (four) of allpass stages, there is no difference.) In discrete time, the general first-order allpass has the transfer function

$$\hbox{AP}_{1}^{\,g_i} \isdef \frac{g_i + z^{-1}}{1 + g_i z^{-1}}.$$

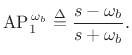
We now consider the analog and digital cases, respectively.