Classic Virtual Analog Phase Shifters

To create a virtual analog phaser, following closely the design of typical analog phasers, we must translate each first-order allpass to the digital domain. Working with the transfer function, we must map from $s$ plane to the $z$ plane. There are several ways to accomplish this goal [365]. However, in this case, an excellent choice is the bilinear transform (see §7.3.2), defined by

$$s \eqsp c\frac{z-1}{z+1} \protect$$ (9.20)

where $c$ is chosen to map one particular frequency to exactly where it belongs. In this case, $c$ can be chosen for each section to map the break frequency of the section to exactly where it belongs on the digital frequency axis. The relation between analog frequency $\omega_a$ and digital frequency $\omega_d$ follows immediately from Eq.(8.20) as

$$\begin{eqnarray*} j\omega_a &=& c\frac{e^{j\omega_d T}-1}{e^{j\omega_d T}+1} \eqsp c\frac{e^{j\omega_d T/2}\left(e^{j\omega_d T/2}-e^{-j\omega_d T/2}\right)}{e^{j\omega_d T/2}\left(e^{j\omega_d T/2}+e^{-j\omega_d T/2}\right)}\\ [5pt] &=& jc\frac{\sin(\omega_dT/2)}{\cos(\omega_dT/2)} \eqsp jc\tan(\omega_dT/2). \end{eqnarray*}$$

Thus, given a particular desired break-frequency $\omega_a=\omega_d=\omega_b$ , we can set

$$c \eqsp \omega_b\cot\left(\frac{\omega_bT}{2}\right).$$

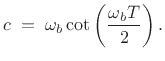
Recall from Eq.(8.19) that the transfer function of the first-order analog allpass filter is given by

$$H_a(s) \eqsp \frac{s-\omega_b}{s+\omega_b}$$

where $\omega_b$ is the break frequency. Applying the general bilinear transformation Eq.(8.20) gives

$$H_d(z) \eqsp H_a\left(c\frac{1-z^{-1}}{1+z^{-1}}\right) \eqsp \frac{c\left(\frac{1-z^{-1}}{1+z^{-1}}\right) - \omega_b}{c\left(\frac{1-z^{-1}}{1+z^{-1}}\right) + \omega_b}\\ \eqsp \frac{p_d-z^{-1}}{1-p_dz^{-1}}$$

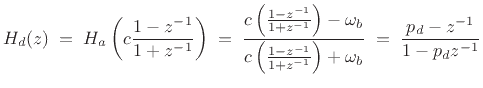
where we have denoted the pole of the digital allpass by

$$p_d\isdefs \frac{c-\omega_b}{c+\omega_b} \eqsp \frac{1-\tan(\omega_bT/2)}{1+\tan(\omega_bT/2)} \;\approx\; \frac{1-\omega_bT/2}{1+\omega_bT/2} \;\approx\; 1-\omega_bT.$$

Figure 8.25 shows the digital phaser response curves corresponding to the analog response curves in Fig.8.24. While the break frequencies are preserved by construction, the notches have moved slightly, although this is not visible from the plots. An overlay of the total phase of the analog and digital allpass chains is shown in Fig.8.26. We see that the phase responses of the analog and digital allpass chains diverge visibly only above 9 kHz. The analog phase response approaches zero in the limit as $\omega_a\to\infty$ , while the digital phase response reaches zero at half the sampling rate, $10$ kHz in this case. This is a good example of when the bilinear transform performs very well.

Figure 8.25: (a) Phase responses of first-order digital allpass sections with break frequencies at 100, 200, 400, and 800 Hz, with the sampling rate set to 20,000 Hz. (b) Corresponding phaser amplitude response.

Figure 8.26: Phase response of four first-order allpass sections in series -- analog and digital cases overlaid.

In general, the bilinear transform works well to digitize feedforward analog structures in which the high-frequency warping is acceptable. When frequency warping is excessive, it can be alleviated by the use of oversampling; for example, the slight visible deviation in Fig.8.26 below 10 kHz can be largely eliminated by increasing the sampling rate by 15% or so. See the case of digitizing the Moog VCF for an example in which the presence of feedback in the analog circuit leads to a delay-free loop in the digitized system [482,480].