Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
This all makes sense, but what about those 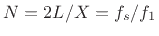 off-diagonal terms in
off-diagonal terms in
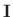 ? Consider the vector angular momentum (§B.4.14):
? Consider the vector angular momentum (§B.4.14):
We see that the off-diagonal terms 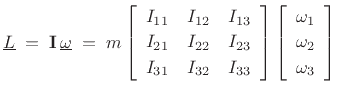 correspond to a
coupling of rotation about
correspond to a
coupling of rotation about
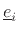 with rotation about
with rotation about
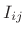 .
That is, there is a component of moment-of-inertia
.
That is, there is a component of moment-of-inertia 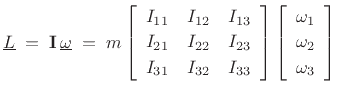 that is
contributed (or subtracted, as we saw above for
that is
contributed (or subtracted, as we saw above for
![$ \underline{\omega}=[1,1,0]^T$](img2914.png) ) when both
) when both 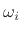 and
and
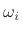 are nonzero. These cross-terms can be eliminated by
diagonalizing the matrix [452],B.25as discussed further in the next section.
are nonzero. These cross-terms can be eliminated by
diagonalizing the matrix [452],B.25as discussed further in the next section.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() off-diagonal terms in
off-diagonal terms in
![]() ? Consider the vector angular momentum (§B.4.14):
? Consider the vector angular momentum (§B.4.14):
![$\displaystyle \underline{L}\eqsp \mathbf{I}\,\underline{\omega}\eqsp
m\left[\begin{array}{ccc}
I_{11} & I_{12} & I_{13}\\ [2pt]
I_{21} & I_{22} & I_{23}\\ [2pt]
I_{31} & I_{32} & I_{33}
\end{array}\right]
\left[\begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](img2911.png)