Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Principal Axes of Rotation
A principal axis of rotation (or principal direction) is
an eigenvector of the mass moment of inertia tensor (introduced
in the previous section) defined relative to some point (typically the
center of mass). The corresponding eigenvalues are called the
principal moments of inertia.
Because the moment of inertia tensor is defined relative to the point
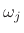 in the space, the principal axes all pass through that point
(usually the center of mass).
in the space, the principal axes all pass through that point
(usually the center of mass).
As derived above (§B.4.14), the angular momentum vector is given by
the moment of inertia tensor times the angular-velocity vector:
If
 is an eigenvector of
is an eigenvector of
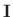 , then we have
, then we have
where the (scalar) eigenvalue 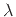 is called a principal moment of
inertia. If we set the rigid body assocated with
is called a principal moment of
inertia. If we set the rigid body assocated with
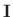 rotating
about the axis
rotating
about the axis
 , then
, then 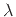 is the mass moment of inertia of
the body for that rotation. As will become clear below, there are
always three mutually orthogonal principal axes of rotation, and three
corresponding principal moments of inertia (in 3D space, of course).
is the mass moment of inertia of
the body for that rotation. As will become clear below, there are
always three mutually orthogonal principal axes of rotation, and three
corresponding principal moments of inertia (in 3D space, of course).
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() in the space, the principal axes all pass through that point
(usually the center of mass).
in the space, the principal axes all pass through that point
(usually the center of mass).