Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Now let the mass  be located at
be located at
![$ \underline{x}=[1,1,0]^T$](img2901.png) so that
so that
We expect
![$ \underline{\omega}=[1,1,0]$](img2903.png) to yield zero for the moment of inertia, and
sure enough
to yield zero for the moment of inertia, and
sure enough
 . Similarly, the vector angular
momentum is zero, since
. Similarly, the vector angular
momentum is zero, since
 .
.
For
![$ \underline{\omega}=[1,0,0]^T$](img2906.png) , the result is
, the result is
which makes sense because the distance from the axis
 to
to
 is one. The same result is obtained for rotation about
is one. The same result is obtained for rotation about
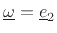 .
For
.
For
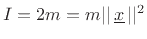 , however, the result is
, however, the result is
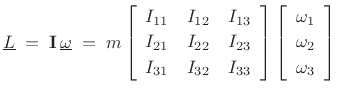 , as
expect.
, as
expect.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() be located at
be located at
![]() so that
so that
![\begin{eqnarray*}
\mathbf{I}&=& m \left(\left\Vert\,\underline{x}\,\right\Vert^2\mathbf{E}-\underline{x}\underline{x}^T\right) \eqsp
m\left(2\mathbf{E}-\left[\begin{array}{ccc}
1 & 1 & 0\\ [2pt]
1 & 1 & 0\\ [2pt]
0 & 0 & 0
\end{array}\right]\right)\\ [5pt]
&=& m\left[\begin{array}{rrr}
1 & -1 & 0\\ [2pt]
-1 & 1 & 0\\ [2pt]
0 & 0 & 2
\end{array}\right].
\end{eqnarray*}](img2902.png)
![]() to yield zero for the moment of inertia, and
sure enough
to yield zero for the moment of inertia, and
sure enough
![]() . Similarly, the vector angular
momentum is zero, since
. Similarly, the vector angular
momentum is zero, since
![]() .
.
![]() , the result is
, the result is
![\begin{displaymath}
\mathbf{I}\eqsp
\begin{array}{r}\left[\begin{array}{ccc} 1 & 0 & 0\end{array}\right]\\ [2pt]{}\\ [2pt]{}\end{array}\left[\begin{array}{rrr}
1 & -1 & 0\\ [2pt]
-1 & 1 & 0\\ [2pt]
0 & 0 & 2
\end{array}\right]
\left[\begin{array}{c} 1 \\ [2pt] 0 \\ [2pt] 0\end{array}\right]m = m,
\end{displaymath}](img2907.png)