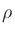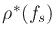Use of a bilinear
conformal map to achieve a
frequency warping nearly
identical to that of the
Bark frequency scale is described. Because the
map takes the unit circle to itself, its form is that of the
transfer
function of a first-order
allpass filter. Since it is a first-order map,
it preserves the model order of rational systems, making it a valuable
frequency warping technique for use in audio
filter design.
A closed-form weighted-
equation-error method is derived which computes the
optimal mapping coefficient as a function of
sampling rate, and the
solution is shown to be generally indistinguishable from the optimal
least-squares solution. The optimal Chebyshev mapping is also found to be
essentially identical to the optimal least-squares solution. The
expression
0.8517*sqrt(atan(0.06583*Fs))-0.1916 is shown to accurately approximate the optimal
allpass coefficient as a function of
sampling rate Fs in kHz for sampling
rates greater than 1 kHz. A
filter design example is included which
illustrates improvements due to carrying out the design over a
Bark scale.
Corresponding results are also given and compared for approximating the
related ``
equivalent rectangular bandwidth (
ERB) scale'' of Moore and
Glasberg using a first-order allpass transformation. Due to the higher
frequency resolution called for by the
ERB scale, particularly at low
frequencies, the first-order conformal map is less able to follow the
desired mapping, and the error is two to three times greater than the
Bark-scale case, depending on the sampling rate.