Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
With the increasing use of frequency-domain techniques in audio signal
processing applications such as audio compression, there is increasing
emphasis on psychoacoustic-based spectral measures
[36,2,11,12]. One of the
classic approaches is to analyze and process signal spectra over the
Bark frequency scale (also called ``critical band rate'')
[41,42,39,21,7].
Based on the results of many psychoacoustic experiments, the Bark
scale is defined so that the critical bands of human hearing have a
width of one Bark. By representing spectral energy (in dB) over the
Bark scale, a closer correspondence is obtained with spectral
information processing in the ear.
The bilinear conformal map, defined by the substitution
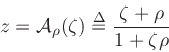 |
(1) |
takes the unit circle in the z plane to the unit circle in the
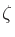 plane2 in such a way that, for
plane2 in such a way that, for 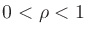 ,
low frequencies are stretched and high frequencies are compressed, as
in a transformation from frequency in Hertz to the Bark scale.
Because the conformal map
,
low frequencies are stretched and high frequencies are compressed, as
in a transformation from frequency in Hertz to the Bark scale.
Because the conformal map
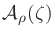 is identical in form to a
first-order allpass transfer function (having a pole at
is identical in form to a
first-order allpass transfer function (having a pole at
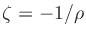 ), we also call it the first-order allpass
transformation, and
), we also call it the first-order allpass
transformation, and 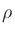 the allpass coefficient.
the allpass coefficient.
Since the allpass mapping possesses only a single degree of freedom, we
have no reason to expect a particularly good match to the Bark frequency
warping, even for an optimal choice of 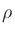 . It turns out, however, that
the match is surprisingly good over a wide range of sampling rates,
as illustrated in Fig.1 for a sampling rate of 31 kHz. The fit
is so good, in fact, that there is almost no difference between the optimal
least-squares and optimal Chebyshev approximations, as the figure shows.
The purpose of this paper is to spread awareness of this useful fact and to
present new methods for computing the optimal warping parameter
. It turns out, however, that
the match is surprisingly good over a wide range of sampling rates,
as illustrated in Fig.1 for a sampling rate of 31 kHz. The fit
is so good, in fact, that there is almost no difference between the optimal
least-squares and optimal Chebyshev approximations, as the figure shows.
The purpose of this paper is to spread awareness of this useful fact and to
present new methods for computing the optimal warping parameter 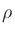 as a
function of sampling rate.
as a
function of sampling rate.
Figure 1:
Bark and allpass frequency warpings at a
sampling rate of 31 kHz (the highest possible without extrapolating
the published Bark scale bandlimits). a) Bark frequency warping
viewed as a conformal mapping of the interval ![$[0,\pi ]$](img1.png) to itself on
the unit circle. b) Same mapping interpreted as an auditory frequency
warping from Hz to Barks; the legend shown in plot a) also applies to
plot b). The legend additionally displays the optimal allpass
parameter
to itself on
the unit circle. b) Same mapping interpreted as an auditory frequency
warping from Hz to Barks; the legend shown in plot a) also applies to
plot b). The legend additionally displays the optimal allpass
parameter 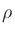 used for each map. The discrete band-edges which
define the Bark scale are plotted as circles. The optimal Chebyshev
(solid), least-squares (dashed), and weighted equation-error
(dot-dashed) allpass parameters produce mappings which are nearly
identical. Also plotted (dotted) is the mapping based on an allpass
parameter given by an analytic expression in terms of the sampling
rate, which will be described. It should be pointed out that the fit
improves as the sampling rate is decreased.
used for each map. The discrete band-edges which
define the Bark scale are plotted as circles. The optimal Chebyshev
(solid), least-squares (dashed), and weighted equation-error
(dot-dashed) allpass parameters produce mappings which are nearly
identical. Also plotted (dotted) is the mapping based on an allpass
parameter given by an analytic expression in terms of the sampling
rate, which will be described. It should be pointed out that the fit
improves as the sampling rate is decreased.
![\includegraphics[scale=0.8]{eps/fitlogf}](img15.png) |
Subsections
Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bbt.pdf
[Comment on this page via email]
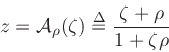
![]() . It turns out, however, that
the match is surprisingly good over a wide range of sampling rates,
as illustrated in Fig.1 for a sampling rate of 31 kHz. The fit
is so good, in fact, that there is almost no difference between the optimal
least-squares and optimal Chebyshev approximations, as the figure shows.
The purpose of this paper is to spread awareness of this useful fact and to
present new methods for computing the optimal warping parameter
. It turns out, however, that
the match is surprisingly good over a wide range of sampling rates,
as illustrated in Fig.1 for a sampling rate of 31 kHz. The fit
is so good, in fact, that there is almost no difference between the optimal
least-squares and optimal Chebyshev approximations, as the figure shows.
The purpose of this paper is to spread awareness of this useful fact and to
present new methods for computing the optimal warping parameter ![]() as a
function of sampling rate.
as a
function of sampling rate.
![\includegraphics[scale=0.8]{eps/fitlogf}](img15.png)