... Abel¹

Work supported in part by San Jose State University Cooperative Agreement NCC-2-327.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... plane²

Note that the image of the conformal map corresponds to the domain variable 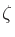$\zeta$ of the allpass transformation, while the input of the map corresponds to the range variable z.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... desired.³

In general, the unit circle is mapped once to itself by any allpass transformation for which the number of poles N_p minus the number of zeros N_z inside the unit circle is |N_p-N_z|=1. Therefore, higher order allpass transfer functions can be used having N_p poles inside the unit circle, say, and $N_z = N_p\pm 1$ poles outside the unit circle. However, such a transformation cannot be used for audio digital filter design, our principle application, because it results in an unstable final filter $H^*[{\cal A}_{-\rho }(z)]$. It similarly cannot be used in any applications requiring time-domain implementation of the unstable allpass filter in place of a unit delay element.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Barks⁴

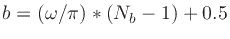The normalized warped-frequency interval $\omega\in[0,\pi]$ was converted to Barks b by the affine transformation $b = (\omega/\pi)*(N_b-1)+0.5$, where N_b is the number of Bark bands in use. For example, N_b=25 for a 31 kHz sampling rate.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...JOST:⁵

Matlab functions bark2lin.m and lin2bark.m for transforming between linear and bark-warped frequency representations are available on the internet at http://ccrma.stanford.edu/~jos/bbt/bbt.html.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.