Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
This subsection provides further details on the arctangent approximation
for the optimal allpass coefficient as a function of sampling rate.
Compared with other spline or polynomial approximations, the arctangent
form
![\begin{displaymath}
\rho _{\mathbf\gamma}(f_s) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\max\left\{0,\gamma_1\left[{2\over\pi}\arctan(\gamma_2f_s)\right]^{{1\over2}}+\gamma_3 \right\}
\end{displaymath}](img115.png) |
(23) |
was found to provide a more parsimonious expression at a given accuracy
level. The idea was that the arctangent function provided a mapping from
the interval 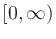 , the domain of fs, to the interval [0,1),
the range of
, the domain of fs, to the interval [0,1),
the range of 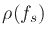 . The additive component
. The additive component 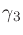 allowed
allowed
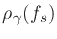 to be zero at smaller sampling rates, where the Bark scale is
linear with frequency. As an additional benefit, the arctangent expression
was easily inverted to give sampling rate fs in terms of the allpass
coefficient
to be zero at smaller sampling rates, where the Bark scale is
linear with frequency. As an additional benefit, the arctangent expression
was easily inverted to give sampling rate fs in terms of the allpass
coefficient
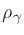 :
:
![\begin{displaymath}
f_s= {1\over \gamma_2}\tan\left[{\pi\over2} \left(\frac{\rho _{\mathbf\gamma}- \gamma_3}{\gamma_1}\right)^2\right].
\end{displaymath}](img121.png) |
(24) |
To obtain the optimal arctangent form
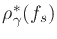 , the expression for
, the expression for
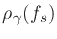 in Eq.(23) was optimized with respect to its free
parameters
in Eq.(23) was optimized with respect to its free
parameters
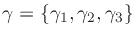 to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
![\begin{displaymath}
\rho ^*_{\mathbf\gamma}(f_s) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\mbox{Arg}\left[\min_{{\mathbf\gamma}}\left\{\left\Vert\,\rho ^*_\infty(f_s) - \rho _{\mathbf\gamma}(f_s)\,\right\Vert _\infty\right\}\right].
\end{displaymath}](img123.png) |
(25) |
For a Bark warping, the optimized arctangent formula was found to be
![\begin{displaymath}
\rho ^*_{\mathbf\gamma}(f_s) = 1.0674\left[{2\over\pi}\arctan(0.06583f_s)\right]^{{1\over2}}-0.1916,
\end{displaymath}](img124.png) |
(26) |
where fs is expressed in units of kHz. This formula is plotted along
with the various optimal 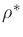 curves in Fig.4a, and the
approximation error is shown in Fig.4b. It is extremely accurate
below 15 kHz and near 40 kHz, and adds generally less than 0.1 Bark to the
peak error at other sampling rates. The rms error versus sampling rate is
very close to optimal at all sampling rates, as Fig.5 also
shows.
curves in Fig.4a, and the
approximation error is shown in Fig.4b. It is extremely accurate
below 15 kHz and near 40 kHz, and adds generally less than 0.1 Bark to the
peak error at other sampling rates. The rms error versus sampling rate is
very close to optimal at all sampling rates, as Fig.5 also
shows.
When the optimality criterion is chosen to minimize relative bandwidth
mapping error (relative map slope error), the arctangent
formula optimization yields
![\begin{displaymath}
\rho ^*_{\mathbf\gamma}(f_s) = 1.0480\left[{2\over\pi}\arctan(0.07212f_s)\right]^{{1\over2}}-0.1957.
\end{displaymath}](img125.png) |
(27) |
The performance of this formula is shown in Fig.9. It tends
to follow the performance of the optimal least squares map parameter even
though the peak parameter error was minimized relative to the optimal
Chebyshev map. At 54 kHz there is an additional 3% bandwidth error due to
the arctangent approximation, and near 10 kHz the additional error is about
4%; at other sampling rates, the performance of the RBME arctangent
approximation is better, and like Eq.(26), it is extremely accurate
at 41 kHz.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bbt.pdf
[Comment on this page via email]
![\begin{displaymath}
f_s= {1\over \gamma_2}\tan\left[{\pi\over2} \left(\frac{\rho _{\mathbf\gamma}- \gamma_3}{\gamma_1}\right)^2\right].
\end{displaymath}](img121.png)
![]() , the expression for
, the expression for
![]() in Eq.(23) was optimized with respect to its free
parameters
in Eq.(23) was optimized with respect to its free
parameters
![]() to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
to match the optimal
Chebyshev allpass coefficient as a function of sampling rate:
![\begin{displaymath}
\rho ^*_{\mathbf\gamma}(f_s) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\mbox{Arg}\left[\min_{{\mathbf\gamma}}\left\{\left\Vert\,\rho ^*_\infty(f_s) - \rho _{\mathbf\gamma}(f_s)\,\right\Vert _\infty\right\}\right].
\end{displaymath}](img123.png)