Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Our goal is to find the allpass coefficient 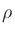 such that the
frequency mapping
such that the
frequency mapping
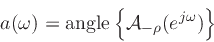 |
(5) |
best approximates the Bark scale 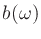 for a given sampling rate
fs. (Note that the frequencies
for a given sampling rate
fs. (Note that the frequencies 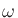 ,
, 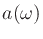 , and
, and 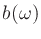 are all expressed in radians per sample, so that a frequency of half
of the sampling rate corresponds to a value of
are all expressed in radians per sample, so that a frequency of half
of the sampling rate corresponds to a value of 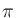 .)
.)
Using squared frequency errors to gauge the fit between 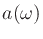 and
its Bark warped counterpart, the optimal mapping parameter
and
its Bark warped counterpart, the optimal mapping parameter 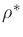 may
be written as
may
be written as
![\begin{displaymath}
\rho ^*= \mbox{Arg}\left[\min_{\rho }\left\{\left\Vert\,a(\omega )- b(\omega )\,\right\Vert\right\}\right],
\end{displaymath}](img39.png) |
(6) |
where
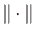 represents the L2 norm.
(We use the superscript `
represents the L2 norm.
(We use the superscript ` ' to denote optimality in some sense.)
Unfortunately, the frequency error
' to denote optimality in some sense.)
Unfortunately, the frequency error
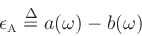 |
(7) |
is nonlinear in 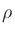 , and its norm is not easily minimized directly.
It turns out, however, that a related error,
, and its norm is not easily minimized directly.
It turns out, however, that a related error,
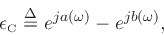 |
(8) |
has a norm which is more amenable to minimization. The first issue we
address is how the minimizers of
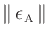 and
and
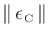 are
related.
are
related.
Figure 2:
Frequency Map Errors
![\includegraphics[scale=0.5]{eps/eaec}](img46.png) |
Denote by 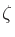 and
and 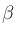 the complex representations of the
frequencies
the complex representations of the
frequencies 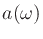 and
and 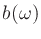 on the unit circle,
on the unit circle,
 |
(9) |
As seen in Fig.2, the absolute frequency error
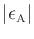 is
the arc length between the points
is
the arc length between the points 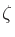 and
and 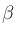 , whereas
, whereas
 is the chord length or distance:
is the chord length or distance:
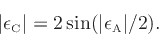 |
(10) |
The desired arc length error
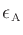 gives more weight to large errors
than the chord length error
gives more weight to large errors
than the chord length error
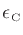 ; however, in the presence of small
discrepancies between
; however, in the presence of small
discrepancies between 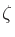 and
and 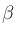 , the absolute errors are
very similar,
, the absolute errors are
very similar,
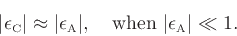 |
(11) |
Accordingly, essentially the same 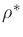 results from minimizing
results from minimizing
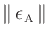 or
or
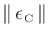 when the fit is uniformly good over
frequency.
when the fit is uniformly good over
frequency.
The error
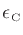 is also nonlinear in the parameter
is also nonlinear in the parameter 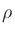 , and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [17]. Consider mapping
the frequency
, and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [17]. Consider mapping
the frequency
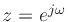 via the allpass transformation
via the allpass transformation
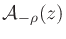 ,
,
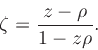 |
(12) |
Now, multiply Eq.(12) by the denominator 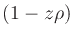 , and
substitute
, and
substitute
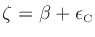 from Eq.(8), to get
from Eq.(8), to get
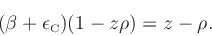 |
(13) |
Rearranging terms, we have
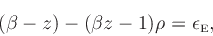 |
(14) |
where
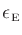 is an equation error defined by
is an equation error defined by
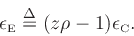 |
(15) |
Figure 3:
Geometric Interpretation of Equation Error
![\includegraphics[scale=0.5]{eps/ee}](img64.png) |
Referring to Fig.3, note that the equation error is the
difference between the unit circle chord 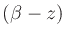 and the
and the
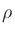 circle chord
circle chord
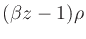 . The average of the input and
Bark warped angles
. The average of the input and
Bark warped angles
![$\left[b(\omega )+\omega \right]/2$](img67.png) bisects both these chords,
and therefore the chords are parallel. The equation error may then be
interpreted as the difference in chord lengths, rotated to the angle
bisects both these chords,
and therefore the chords are parallel. The equation error may then be
interpreted as the difference in chord lengths, rotated to the angle
![$\left[b(\omega )+\omega \right]/2 + \pi/2$](img68.png) . This suggests defining a rotated
equation error which is real valued. Multiply Eq.(14) by
. This suggests defining a rotated
equation error which is real valued. Multiply Eq.(14) by
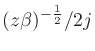 to obtain
to obtain
![\begin{displaymath}
\sin\left[\frac{b(\omega )-\omega }{2}\right]
- \rho \sin\left[\frac{b(\omega )+\omega }{2}\right] = \epsilon _{\mbox{\tiny R}},
\end{displaymath}](img70.png) |
(16) |
where the rotated equation error
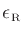 is defined by
is defined by
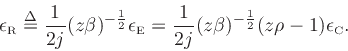 |
(17) |
The rotated equation error
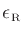 is linear in the unknown
is linear in the unknown 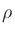 , and
its norm minimizer is easily expressed in closed form. Denote by
, and
its norm minimizer is easily expressed in closed form. Denote by
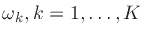 a set of frequencies corresponding to Bark
frequencies
a set of frequencies corresponding to Bark
frequencies 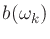 , and by
, and by
 and
and
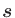 the columns
the columns
Then Eq.(16) becomes
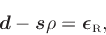 |
(20) |
where
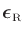 is a column of rotated equation errors.
Eq.(20) is now in the form of a standard least squares problem.
As is well known [17,34], the solution
is a column of rotated equation errors.
Eq.(20) is now in the form of a standard least squares problem.
As is well known [17,34], the solution 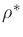 which
minimizes the weighted sum of squared errors,
which
minimizes the weighted sum of squared errors,
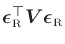 , the matrix
, the matrix
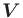 being an arbitrary positive-definite weighting, may be obtained by
premultiplying both sides of
Eq.(20) by
being an arbitrary positive-definite weighting, may be obtained by
premultiplying both sides of
Eq.(20) by
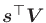 and solving for
and solving for 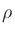 , noting that at
, noting that at
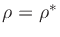 ,
,
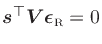 by the orthogonality principle. Doing this yields the
optimal weighted least-squares conformal map parameter
by the orthogonality principle. Doing this yields the
optimal weighted least-squares conformal map parameter
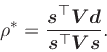 |
(21) |
If the weighting matrix
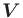 is diagonal with kth diagonal
element
is diagonal with kth diagonal
element
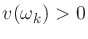 , then the weighted least-squares
solution Eq.(21) reduces to
, then the weighted least-squares
solution Eq.(21) reduces to
where we have used Equations
Eq.(18) and Eq.(19),
and the trigonometric identities
to simplify the numerator and denominator, respectively.
It remains to choose a weighting matrix
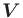 . Recall that we initially
wanted to minimize the sum of squared chord-length errors
. Recall that we initially
wanted to minimize the sum of squared chord-length errors
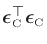 .
The rotated equation error
.
The rotated equation error
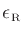 is proportional to the chord length error
is proportional to the chord length error
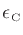 , viz. Eq.(17), and it is easily verified that when
, viz. Eq.(17), and it is easily verified that when
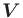 is
diagonal with kth diagonal element
is
diagonal with kth diagonal element
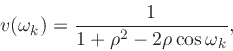 |
(22) |
the chord length error and the weighted equation error coincide.
Thus, with this diagonal weighting matrix, the solution Eq.(21)
minimizes the chord-length error norm.
Note that the desired weighting depends on the unknown map parameter 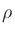 .
To overcome this difficulty, we suggest first estimating
.
To overcome this difficulty, we suggest first estimating 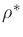 using
using
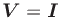 , where
, where
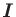 denotes the identity matrix, and then computing
denotes the identity matrix, and then computing
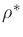 using the weighting Eq.(22) based on the unweighted solution.
This is analogous to the Steiglitz-McBride algorithm for converting an
equation-error minimizer to the more desired ``output-error'' minimizer
using an iteratively computed weight function
[16].
using the weighting Eq.(22) based on the unweighted solution.
This is analogous to the Steiglitz-McBride algorithm for converting an
equation-error minimizer to the more desired ``output-error'' minimizer
using an iteratively computed weight function
[16].
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bbt.pdf
[Comment on this page via email]
![]() such that the
frequency mapping
such that the
frequency mapping
![]() and
its Bark warped counterpart, the optimal mapping parameter
and
its Bark warped counterpart, the optimal mapping parameter ![]() may
be written as
may
be written as
![\begin{displaymath}
\rho ^*= \mbox{Arg}\left[\min_{\rho }\left\{\left\Vert\,a(\omega )- b(\omega )\,\right\Vert\right\}\right],
\end{displaymath}](img39.png)
![]() and
and ![]() the complex representations of the
frequencies
the complex representations of the
frequencies ![]() and
and ![]() on the unit circle,
on the unit circle,
![]() is also nonlinear in the parameter
is also nonlinear in the parameter ![]() , and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [17]. Consider mapping
the frequency
, and to find
its norm minimizer, an equation error is introduced, as is
common practice in developing solutions to nonlinear system
identification problems [17]. Consider mapping
the frequency
![]() via the allpass transformation
via the allpass transformation
![]() ,
,
![]() and the
and the
![]() circle chord
circle chord
![]() . The average of the input and
Bark warped angles
. The average of the input and
Bark warped angles
![]() bisects both these chords,
and therefore the chords are parallel. The equation error may then be
interpreted as the difference in chord lengths, rotated to the angle
bisects both these chords,
and therefore the chords are parallel. The equation error may then be
interpreted as the difference in chord lengths, rotated to the angle
![]() . This suggests defining a rotated
equation error which is real valued. Multiply Eq.(14) by
. This suggests defining a rotated
equation error which is real valued. Multiply Eq.(14) by
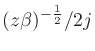 to obtain
to obtain
![]() is linear in the unknown
is linear in the unknown ![]() , and
its norm minimizer is easily expressed in closed form. Denote by
, and
its norm minimizer is easily expressed in closed form. Denote by
![]() a set of frequencies corresponding to Bark
frequencies
a set of frequencies corresponding to Bark
frequencies ![]() , and by
, and by
![]() and
and
![]() the columns
the columns
![\begin{eqnarray*}
\rho ^*&=& \frac{\sum_{k=1}^K
v(\omega _k)
\sin\left[\frac{b(\omega_{k})-\omega_{k}}{2}\right]
\sin\left[\frac{b(\omega_{k})+\omega_{k}}{2}\right]
}{\sum_{k=1}^K
v(\omega _k)\sin^2\left[\frac{b(\omega_{k})+\omega_{k}}{2}\right]} \\
&=& \frac{\sum_{k=1}^{K}
v(\omega _k)
\left\{\cos\left[b(\omega_{k})\right]- \cos(\omega_{k})\right\}}{%
\sum_{k=1}^{K} v(\omega_{k}) \left\{\cos\left[b(\omega_{k}) + \omega_{k}\right]- 1\right\}},
\end{eqnarray*}](img90.png)
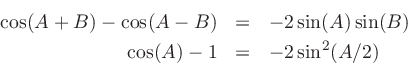
![]() . Recall that we initially
wanted to minimize the sum of squared chord-length errors
. Recall that we initially
wanted to minimize the sum of squared chord-length errors
![]() .
The rotated equation error
.
The rotated equation error
![]() is proportional to the chord length error
is proportional to the chord length error
![]() , viz. Eq.(17), and it is easily verified that when
, viz. Eq.(17), and it is easily verified that when
![]() is
diagonal with kth diagonal element
is
diagonal with kth diagonal element
![]() .
To overcome this difficulty, we suggest first estimating
.
To overcome this difficulty, we suggest first estimating ![]() using
using
![]() , where
, where
![]() denotes the identity matrix, and then computing
denotes the identity matrix, and then computing
![]() using the weighting Eq.(22) based on the unweighted solution.
This is analogous to the Steiglitz-McBride algorithm for converting an
equation-error minimizer to the more desired ``output-error'' minimizer
using an iteratively computed weight function
[16].
using the weighting Eq.(22) based on the unweighted solution.
This is analogous to the Steiglitz-McBride algorithm for converting an
equation-error minimizer to the more desired ``output-error'' minimizer
using an iteratively computed weight function
[16].