Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
In general, if the first  derivatives of a continuous function
derivatives of a continuous function
 exist (i.e., they are finite and uniquely defined), then its
Fourier Transform magnitude is asymptotically proportional to
exist (i.e., they are finite and uniquely defined), then its
Fourier Transform magnitude is asymptotically proportional to
Proof: Look up ``roll-off rate'' in text index.
- Thus, we have the following rule-of-thumb:
(since
 ).
).
- This is also
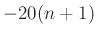 dB per decade.
dB per decade.
- To apply this result, we normally only need to look at the window's
endpoints. The interior of the window is usually
differentiable of all orders.
Examples:
- Amplitude discontinuity

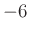 dB/octave roll-off
dB/octave roll-off
- Slope discontinuity

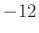 dB/octave roll-off
dB/octave roll-off
- Curvature discontinuity

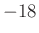 dB/octave roll-off
dB/octave roll-off
For discrete-time windows, the roll-off rate slows down at high
frequencies due to aliasing.
In summary, the DTFT of the 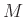 -sample rectangular window is
proportional to the `aliased sinc function':
-sample rectangular window is
proportional to the `aliased sinc function':
Some important points (rect window transform):
- Zero crossings at integer multiples of
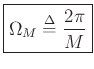
(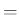 freq. sampling interval used by a length
freq. sampling interval used by a length 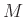 DFT)
DFT)
- Main lobe width is
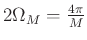
- As
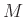 gets bigger, the main-lobe narrows
gets bigger, the main-lobe narrows
(better frequency resolution)
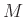 has no effect on the height of the side lobes
has no effect on the height of the side lobes
(Same as the ``Gibbs phenomenon'' for Fourier series)
- First side lobe only 13 dB down from main-lobe peak
- Side lobes roll off at approximately 6dB per octave
- A linear phase term arises when we shift the window to make
it causal, while the window
transform is real in the zero-centered case
(i.e., when the window
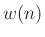 is an even function of
is an even function of  )
)
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Intro421.pdf
Download Intro421_2up.pdf
Download Intro421_4up.pdf
[Comment on this page via email]
![]() derivatives of a continuous function
derivatives of a continuous function
![]() exist (i.e., they are finite and uniquely defined), then its
Fourier Transform magnitude is asymptotically proportional to
exist (i.e., they are finite and uniquely defined), then its
Fourier Transform magnitude is asymptotically proportional to
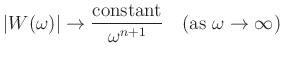
![]() -sample rectangular window is
proportional to the `aliased sinc function':
-sample rectangular window is
proportional to the `aliased sinc function':
![\begin{eqnarray*}
\hbox{asinc}_M(\omega T) &\mathrel{\stackrel{\Delta}{=}}& \frac{\sin(\omega M T / 2)}{M\sin(\omega T/2)} \\ [0.2in]
&\approx& \frac{\sin(\pi fMT)}{M\pi fT} \mathrel{\stackrel{\mathrm{\Delta}}{=}}\mbox{sinc}(fMT)
\end{eqnarray*}](img67.png)