Example of Windowing

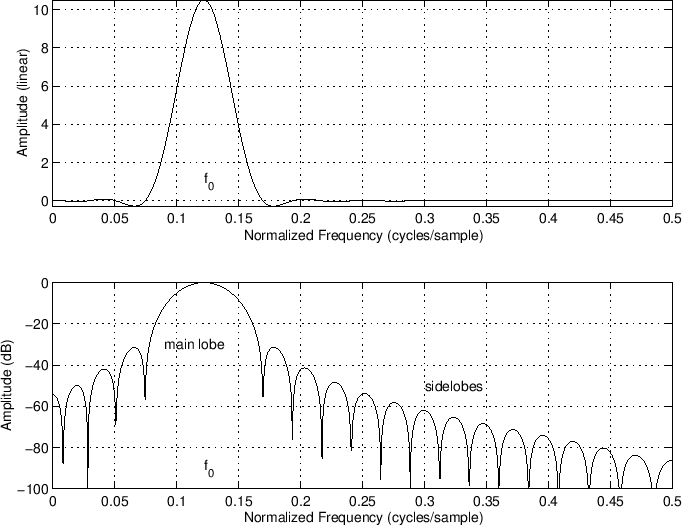
Let's look at a simple example of windowing to demonstrate what happens when we turn an infinite duration signal into a finite duration signal through windowing.

Complex Sinusoid:

$$x(n) = e^{j\omega n T}, \hspace{2cm} 0 \leq \omega T < \pi$$

Notes:

• real part $= \cos(\omega n T)$

• The frequencies present in our signal are only positive. A fancy name for $x(n)$ is an `analytic signal'

This signal is infinite duration. (It doesn't die out as $n$ increases.) In order to end up with a signal which dies out eventually (so we can use the DFT), we need to multiply our signal by a window (which does die out).

Putting all this together, we get the following:

Our original signal (unwindowed, infinite duration), is

$$x(n) = e^{j \omega_0 n T }, \hspace{.5cm} n \in \mathbb{Z}$$

A portion of the real part, $\cos(\omega_0 nT)$ , is plotted below:

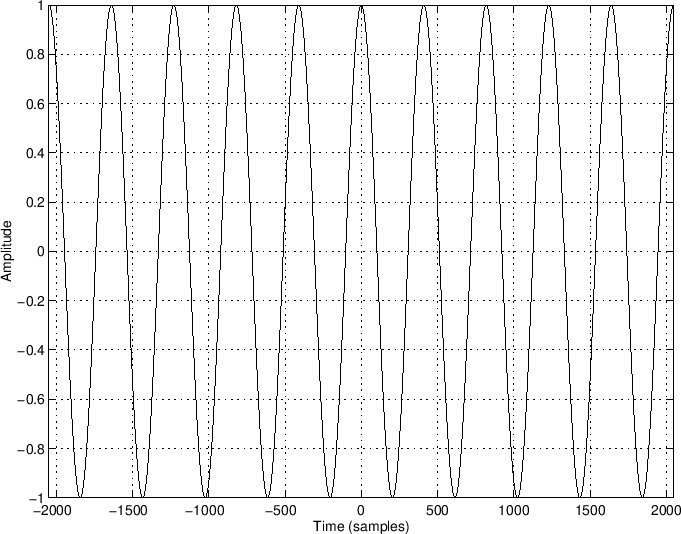
The imaginary part, $\sin(\omega_0 nT)$ , is of course identical but for a 90-degree phase-shift to the right.

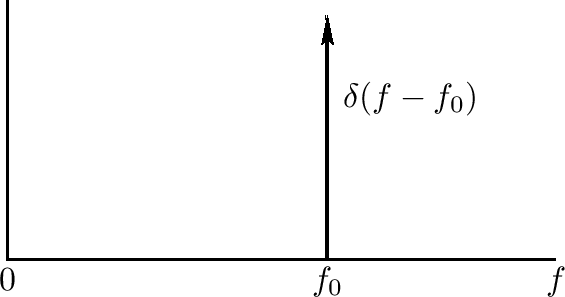
The Fourier Transform of this infinite duration signal is a delta function at $\omega_0$ :

$$X( \omega ) = 2\pi\delta( \omega - \omega_0 ) = \delta(f-f_0)$$

The following is a diagram of a typical window function:

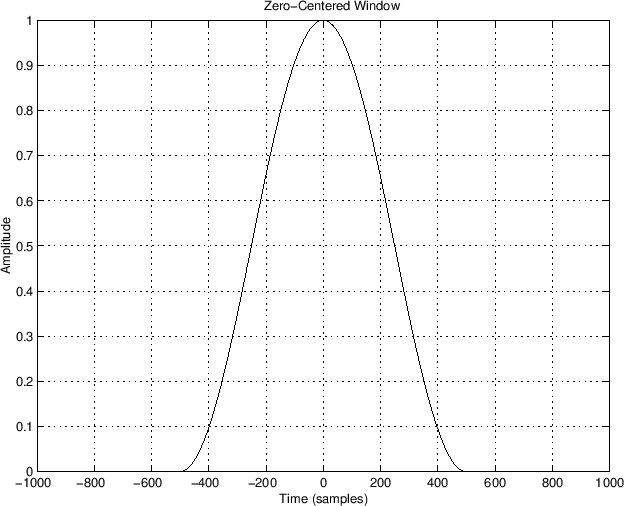
This may be called a ``zero-centered'' (or ``zero phase'', or ``even'') window function, which means its phase in the frequency domain is either zero or $\pi$ , as we will see in detail later. (Recall that a real and even function has a real and even Fourier transform.) The window is also nonnegative, as is typical.

We might also require that our window be zero for negative time. Such a window is said to be `causal'. Causal windows are necessary for real-time processing:

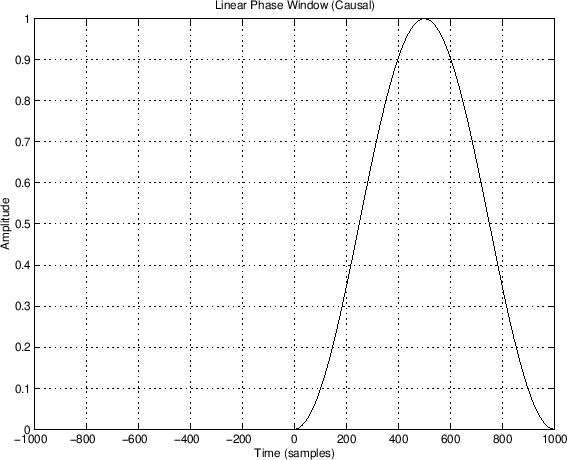
By shifting the original window in time by half its length, we have turned the original non-causal window into a causal window. The Shift property of the Fourier Transform tells us that we have introduced a linear phase term.

The windowed complex sinusoid is:

$$x_w(n) \;=\;w(n)x(n) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;w(n)e^{-j \omega_0 n T} \hspace{1cm} n \in \mathbb{Z}$$

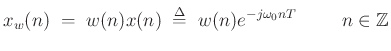
(Note carefully the difference between $w$ and $\omega$ .)

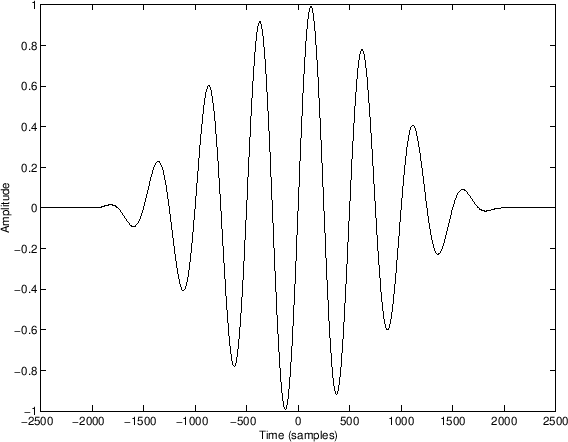
The Convolution Theorem tells us that our multiplication in the time domain results in a convolution in the frequency domain. Hence, in our case, we will obtain the convolution of a delta function at frequency $\omega_0$ , and the transform of the window:

$$X_w(\omega) \;=\;(W \ast X)(\omega) \;=\;W(\omega-\omega_0)$$

The result of convolution with a delta function is the original function, shifted to the location of the delta function. (The delta function is the identity element for convolution.)