Rectangular Window Transform (Cont'd)

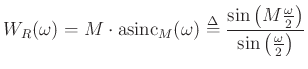
Above, we found the rectangular window transform to be the aliased sinc function:

$$W_R(\omega) = M\cdot \hbox{asinc}_M(\omega) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\frac{\sin\left(M\frac{\omega}{2}\right)}{\sin\left(\frac{\omega}{2}\right)}$$

This (real) result is for the zero-centered rectangular window. For the causal case, a linear phase term appears:

$$W^c_R(\omega) = e^{-j\frac{M-1}{2}\omega}M\hbox{asinc}_M(\omega)$$

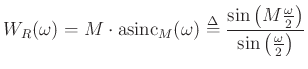
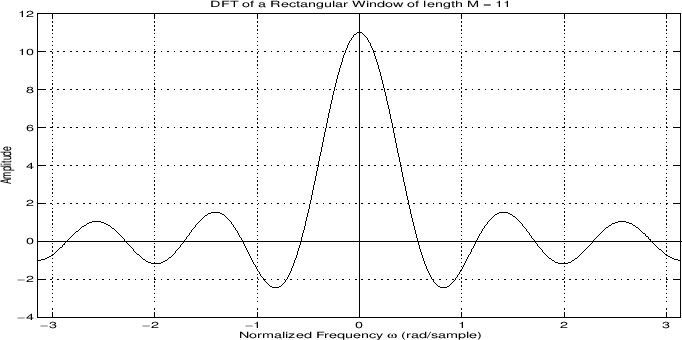
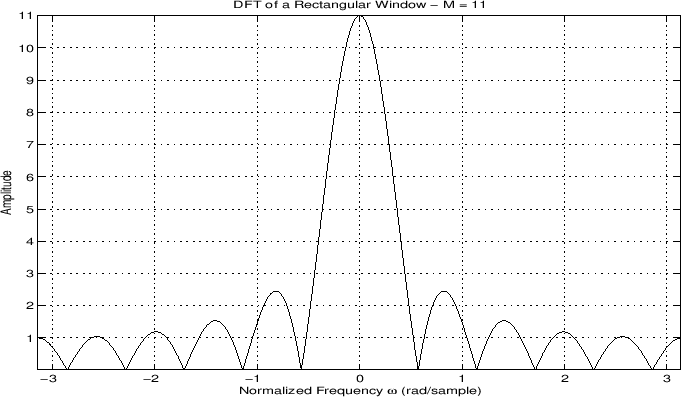
As the sampling rate goes to infinity, the aliased sinc function approaches the regular sinc function

   sinc$$(x) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\frac{\sin(\pi x)}{\pi x}$$

More generally, we may plot both the magnitude and phase of the window transform versus frequency:

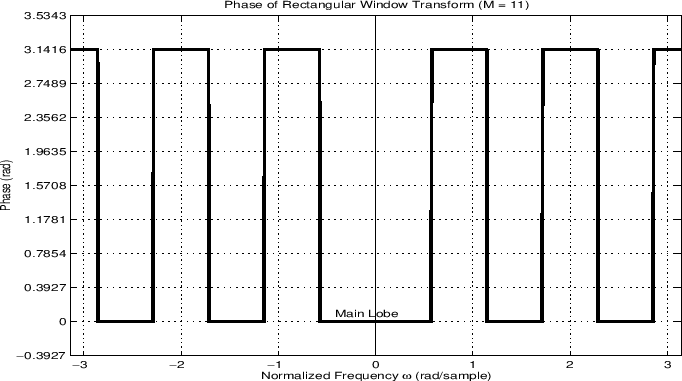
In audio work, we more typically plot the window transform magnitude on a decibel (dB) scale:

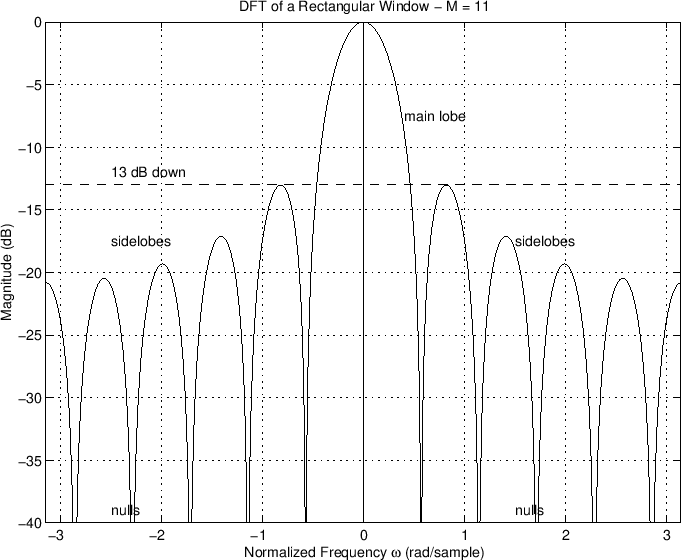
Since the DTFT of the rectangular window approximates the sinc function, it should ``roll off'' at approximately 6 dB per octave, as verified in the log-log plot below:

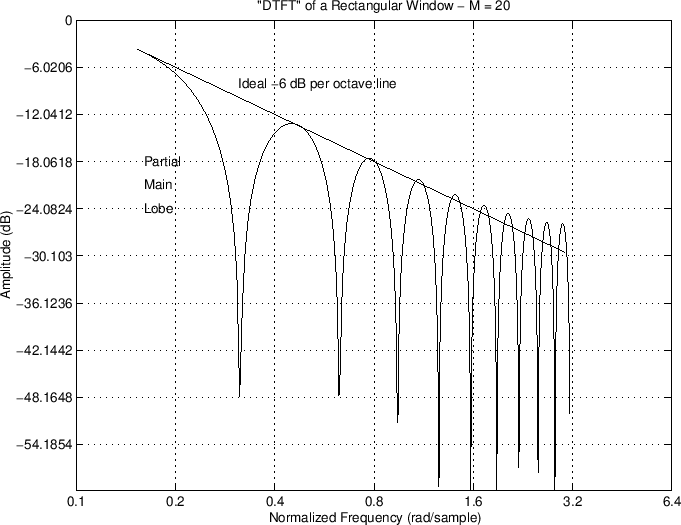
As the sampling rate approaches infinity, the rectangular-window transform ( $\hbox{asinc}$ ) converges exactly to the sinc function. Therefore, the departure of the roll-off from that of the sinc function can be ascribed to aliasing in the frequency domain, due to sampling in the time domain.