![$\displaystyle w_R(n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\{\begin{array}{ll}
1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt]
0, & \hbox{otherwise} \\
\end{array} \right.
$](img40.png)
The rectangular window may be defined as:
![$\displaystyle w_R(n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\{\begin{array}{ll}
1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt]
0, & \hbox{otherwise} \\
\end{array} \right.
$](img40.png)
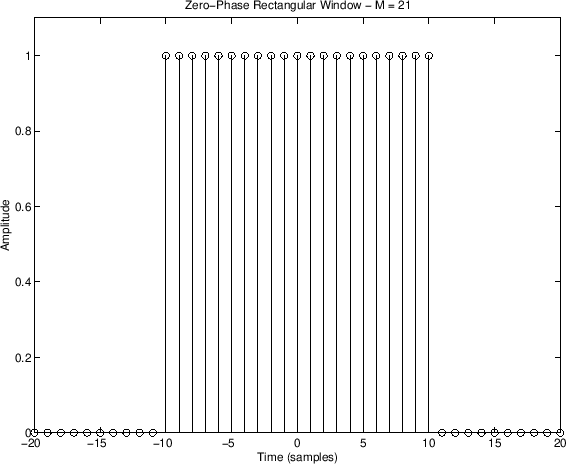
To see what happens in the frequency domain, we need to look at the DTFT of the window:
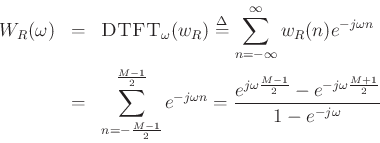
where we used the closed form of a geometric series:
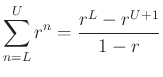
We can factor out linear phase terms from the numerator and denominator of the above expression to get
where
![]() denotes the aliased sinc function.
denotes the aliased sinc function.
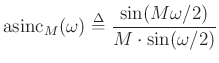
(also called the Dirichlet function)