The Rectangular Window

The (zero-centered) rectangular window may be defined by

$$w_R(n) \isdef \left\{ \begin{array}{ll} 1, & -\frac{M-1}{2} \leq n \leq \frac{M-1}{2} \\ 0, & \mbox{otherwise} \\ \end{array} \right.$$ (4.2)

where $M$ is the window length in samples (assumed odd for now). A plot of the rectangular window appears in Fig.3.1 for length $M=21$ . It is sometimes convenient to define windows so that their dc gain is 1, in which case we would multiply the definition above by $1/M$ .

Figure 3.1: The rectangular window.

To see what happens in the frequency domain, we need to look at the DTFT of the window:

$$\begin{eqnarray*} W_R(\omega ) & = & \hbox{\sc DTFT}_\omega(w_R) \isdef \sum_{n=-\infty}^\infty w_R(n)e^{-j\omega n}, \quad \omega\in[-\pi,\pi) \\ & = & \sum_{n=-\frac{M-1}{2}}^{\frac{M-1}{2}} e^{-j \omega n} = \frac{e^{j \omega \frac{M-1}{2}} - e^{-j \omega \frac{M+1}{2}} }{1 - e^{-j \omega }} \end{eqnarray*}$$

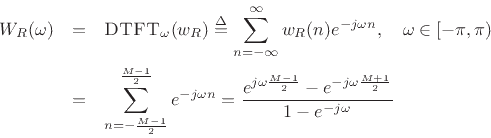
where the last line was derived using the closed form of a geometric series:

$$\sum_{n=L}^U r^n = \frac{ r^L - r^{U+1}}{1-r}$$ (4.3)

We can factor out linear phase terms from the numerator and denominator of the above expression to get

$$W_R(\omega) = \frac{e^{-j \omega \frac{1}{2}}}{e^{-j\omega \frac{1}{2}}} \left[ \frac{ e^{j \omega \frac{M}{2}}-e^{-j\omega\frac{M}{2}}} {e^{j \omega\frac{1}{2}}-e^{-j\omega\frac{1}{2}}} \right]$$

$$= \frac{\sin\left(M\frac{\omega}{2}\right)}{\sin\left(\frac{\omega}{2}\right)} \isdef M\cdot \hbox{asinc}_M(\omega) \protect$$ (4.4)

where $\hbox{asinc}_M(\omega)$ denotes the aliased sinc function:^4.1

$$\hbox{asinc}_M(\omega) \isdef \frac{\sin(M\omega/2)}{M\cdot \sin(\omega/2)} \protect$$ (4.5)

(also called the Dirichlet function [175,72] or periodic sinc function). This (real) result is for the zero-centered rectangular window. For the causal case, a linear phase term appears:

$$W^c_R(\omega) = e^{-j\frac{M-1}{2}\omega} \cdot M \cdot \hbox{asinc}_M(\omega)$$ (4.6)

The term ``aliased sinc function'' refers to the fact that it may be simply obtained by sampling the length-$\tau$ continuous-time rectangular window, which has Fourier transform sinc$(f \tau)\isdeftext \sin(\pi f \tau)/(\pi f\tau)$ (given amplitude $1/\tau$ in the time domain). Sampling at intervals of $T$ seconds in the time domain corresponds to aliasing in the frequency domain over the interval $[0,1/T]$ Hz, and by direct derivation, we have found the result. It is interesting to consider what happens as the window duration increases continuously in the time domain: the magnitude spectrum can only change in discrete jumps as new samples are included, even though it is continuously parametrized in $\tau$ .

As the sampling rate goes to infinity, the aliased sinc function therefore approaches the sinc function

$$(x) \isdef \frac{\sin(\pi x)}{\pi x}. \protect$$ (4.7)

Specifically,

$$\lim_{\stackrel{T\to 0}{MT=\tau}} \hbox{asinc}_M(\omega T) = (\tau f). \protect$$ (4.8)

where $\omega = 2\pi f$ .^4.2

Figure 3.2: Fourier transform of the rectangular window.

Figure 3.2 illustrates $W_R(\omega) = M\cdot\hbox{asinc}_M(\omega)$ for $M=11$ . Note that this is the complete window transform, not just its real part. We obtain real window transforms like this only for zero-centered, symmetric windows. Note that the phase of rectangular-window transform $W_R(\omega)$ is zero for $\vert\omega\vert<2\pi/M$ , which is the width of the main lobe. This is why zero-centered windows are often called zero-phase windows; while the phase actually alternates between 0 and $\pi$ radians, the $\pi$ values occur only within side-lobes which are routinely neglected (in fact, the window is normally designed to ensure that all side-lobes can be neglected).

More generally, we may plot both the magnitude and phase of the window versus frequency, as shown in Figures 3.4 and 3.5 below. In audio work, we more typically plot the window transform magnitude on a decibel (dB) scale, as shown in Fig.3.3 below. It is common to normalize the peak of the dB magnitude to 0 dB, as we have done here.

Figure 3.3: Magnitude (dB) of the rectangular-window transform.

Figure 3.4: Magnitude of the rectangular-window Fourier transform.

Figure 3.5: Phase of the rectangular-window Fourier transform.