


Next: The Waveguide Mesh
Up: The (2+1)D Parallel-plate System
Previous: The (2+1)D Parallel-plate System
The set of PDEs describing a lossless, source-free parallel-plate transmission line in (2+1)D is a direct generalization of system (4.17):
 |
(4.60a) |
Now
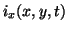 and
and
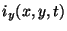 are the components of the current density vector in the
are the components of the current density vector in the  and
and 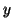 directions, respectively, and
directions, respectively, and 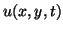 is the voltage between the plates.
is the voltage between the plates. 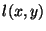 and
and 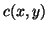 , both assumed positive everywhere, are the inductance and capacitance per unit length.
, both assumed positive everywhere, are the inductance and capacitance per unit length.
If we assume that  and
and  are constant, then as in the (1+1)D case, the set of equations can be reduced to a single second order equation in the voltage alone:
are constant, then as in the (1+1)D case, the set of equations can be reduced to a single second order equation in the voltage alone:
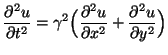 |
(4.61) |
and again, the wave speed 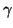 is given by
is given by
The centered difference scheme for system (4.49) also generalizes simply. Define grid functions
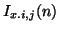 ,
,
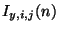 and
and
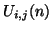 which run over half-integer values of
which run over half-integer values of  ,
, 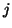 , and
, and  , i.e.,
, i.e.,
We will furthermore assume that the spatial step in the  direction and the
direction and the 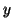 direction are the same and equal to
direction are the same and equal to 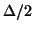 . As before, the time step will be
. As before, the time step will be 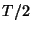 .
We can use the approximations (4.19), as well as an approximation to the derivative in the
.
We can use the approximations (4.19), as well as an approximation to the derivative in the 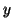 direction,
direction,
where 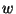 stands for either of
stands for either of 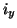 or
or 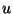 .
We obtain the difference scheme
.
We obtain the difference scheme
where we have written
and
As in the (1+1)D case, it is possible to subdivide the calculation scheme (4.51) into smaller, mutually exclusive subschemes. Using a decimated grid for the variable coefficient difference scheme amounts to rewriting scheme (4.51) as
where we now compute solutions for  ,
, 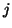 and
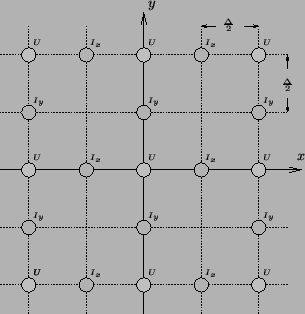
and  integer. The interleaved grid is shown in Figure 4.18; a grey (white) dot at a grid location indicates that the adjacent named variable is to be calculated at times which are even (odd) multiples of
integer. The interleaved grid is shown in Figure 4.18; a grey (white) dot at a grid location indicates that the adjacent named variable is to be calculated at times which are even (odd) multiples of 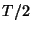 . This interleaved form was originally put forth by Yee [214] in the context of electromagnetic field problems, and forms the basis of the widely used finite-difference time domain (FDTD) family of difference methods [184], which were discussed briefly in §4.1. If system (4.52) is rewritten as a TE or TM system, the interleaved arrangement of the field components also has an interesting physical interpretation as a discrete counterpart to the integral form of Ampere's and Faraday's Laws [184]. This result also extends easily to the discretization of Maxwell's equations in (3+1)D [214]; see §4.10.6 for more details.
. This interleaved form was originally put forth by Yee [214] in the context of electromagnetic field problems, and forms the basis of the widely used finite-difference time domain (FDTD) family of difference methods [184], which were discussed briefly in §4.1. If system (4.52) is rewritten as a TE or TM system, the interleaved arrangement of the field components also has an interesting physical interpretation as a discrete counterpart to the integral form of Ampere's and Faraday's Laws [184]. This result also extends easily to the discretization of Maxwell's equations in (3+1)D [214]; see §4.10.6 for more details.
Figure 4.18:
Interleaved computational grid for the (2+1)D parallel-plate system.
 |
The (2+1)D analogue of (4.23), which holds in the case where  and
and  are constant, is
are constant, is
The magic time step will now be
and (4.53) simplifies to
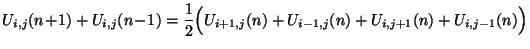 |
(4.66) |
As in (1+1)D, when we are solving the wave equation by centered differences at the magic time step (or at CFL), the calculation further decomposes into two independent calculations; we need only update
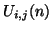 for
for 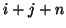 even (or odd). We will examine this interesting decomposition property in detail in Appendix A.
even (or odd). We will examine this interesting decomposition property in detail in Appendix A.



Next: The Waveguide Mesh
Up: The (2+1)D Parallel-plate System
Previous: The (2+1)D Parallel-plate System
Stefan Bilbao
2002-01-22
![]() and
and ![]() are constant, then as in the (1+1)D case, the set of equations can be reduced to a single second order equation in the voltage alone:
are constant, then as in the (1+1)D case, the set of equations can be reduced to a single second order equation in the voltage alone:
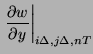
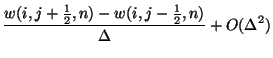
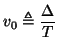
![]() and
and ![]() are constant, is
are constant, is