Scheme (3.18) employs only one difference operator, a second-order accurate approximation
![]() to the operator
to the operator
![]() . While it might be tempting to conclude that the scheme itself will generate a solution which converges to the solution of (3.1) with an error that depends on
. While it might be tempting to conclude that the scheme itself will generate a solution which converges to the solution of (3.1) with an error that depends on ![]() (which is in fact true in this case), the analysis of accuracy of an entire scheme is slightly more subtle than that applied to a single operator in isolation. It is again useful to consider the action of the operator
(which is in fact true in this case), the analysis of accuracy of an entire scheme is slightly more subtle than that applied to a single operator in isolation. It is again useful to consider the action of the operator
![]() on a continuous function
on a continuous function ![]() . In this case, scheme (3.18) may be rewritten as
. In this case, scheme (3.18) may be rewritten as
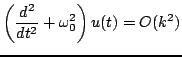 |
(3.33) |
In general, the accuracy of a given scheme will be at least that of the constituent operators; an interesting case study is presented in §3.3.4.