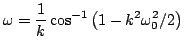Next: Accuracy
Up: A Simple Scheme
Previous: Initialization
Contents
Index
Frequency Domain Analysis
The frequency domain analysis of scheme (3.18) is very similar to that of the simple harmonic oscillator, as outlined in Section 3.1.1. Applying a 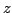 -transformation to (3.19), or, simply inserting a test solution of the form
-transformation to (3.19), or, simply inserting a test solution of the form 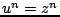 , where
, where
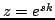 , leads to the characteristic equation
, leads to the characteristic equation
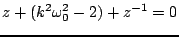 |
(3.22) |
which has the solution
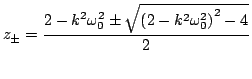 |
(3.23) |
When 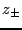 are distinct, the solution to (3.18) will evolve according to
are distinct, the solution to (3.18) will evolve according to
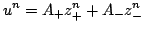 |
(3.24) |
Under the condition
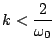 |
(3.25) |
the two roots 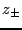 will be complex conjugates of magnitude unity (see §2.3.3 and Problem 2.10), in which case they may be written as
will be complex conjugates of magnitude unity (see §2.3.3 and Problem 2.10), in which case they may be written as
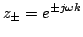 |
(3.26) |
and the solution (3.24) may be rewritten as
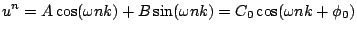 |
(3.27) |
where
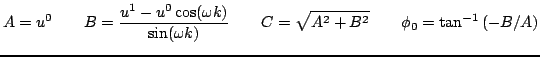 |
(3.28) |
This solution is clearly well-behaved, and resembles the solution to the continuous time SHO, from (3.3). From the form of (3.27), the following bound on the numerical solution size, in terms of the initial conditions and
 follows immediately:
follows immediately:
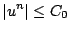 |
(3.29) |
Condition (3.25) may be violated in two different ways. If
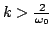 , then the two roots of (
, then the two roots of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) will be real, and one will be of magnitude greater than unity. Thus solution (3.24) will clearly grow exponentially. If
) will be real, and one will be of magnitude greater than unity. Thus solution (3.24) will clearly grow exponentially. If
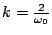 , then the two roots of (3.23) coincide, at
, then the two roots of (3.23) coincide, at
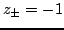 . In this case, the solution (3.24) does not hold, and there will be a term which grows linearly. In neither of the above cases does the solution behave in accordance with (3.3), and its size cannot be bounded in terms of initial conditions alone. Such growth is called numerically unstable (and in the latter case marginally unstable), and condition (3.25) serves as a stability condition.
. In this case, the solution (3.24) does not hold, and there will be a term which grows linearly. In neither of the above cases does the solution behave in accordance with (3.3), and its size cannot be bounded in terms of initial conditions alone. Such growth is called numerically unstable (and in the latter case marginally unstable), and condition (3.25) serves as a stability condition.
Condition (3.25) may be rewritten, using sample rate
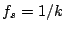 and oscillator frequency
and oscillator frequency
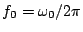 as
as
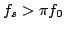 |
(3.30) |
which, from the point of view of sampling theory, is counterintuitive. One would expect that the sampling rate necessary to simulate a sinusoid at frequency 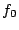 should satisfy
should satisfy
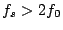 , not the above condition, which is more restrictive. The reason for this is of course that the numerical solution does not in fact oscillate at frequency
, not the above condition, which is more restrictive. The reason for this is of course that the numerical solution does not in fact oscillate at frequency
 , but at frequency
, but at frequency 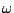 given by
given by
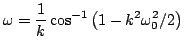 |
(3.31) |
This frequency warping effect is due to approximation error in the finite difference scheme (3.18) itself; such an effect will be generalized to numerical dispersion in distributed problems seen later in this book, and constitutes what is perhaps the largest single disadvantage of using time-domain methods for sound synthesis. Note in particular that
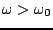 . Perceptually, such an effect will lead to mistuning of ``modes" in a simulation of a musical instrument. There are many means of combating this unwanted effect, perhaps the most crude being to use a higher sampling rate (or smaller value of
. Perceptually, such an effect will lead to mistuning of ``modes" in a simulation of a musical instrument. There are many means of combating this unwanted effect, perhaps the most crude being to use a higher sampling rate (or smaller value of  ; note that frequency
; note that frequency  approaches
approaches
 in the limit as
in the limit as  becomes small). This approach, however, though somewhat standard in the more mainstream simulation community, is not so useful in audio, as the sample rate is generally fixed3.1. Another approach, which will be outlined in Section
becomes small). This approach, however, though somewhat standard in the more mainstream simulation community, is not so useful in audio, as the sample rate is generally fixed3.1. Another approach, which will be outlined in Section ![[*]](file:/usr/share/latex2html/icons/crossref.png) , involves different types of approximations to (3.1), and will be elaborated upon extensively throughout the rest of this book.
, involves different types of approximations to (3.1), and will be elaborated upon extensively throughout the rest of this book.





Next: Accuracy
Up: A Simple Scheme
Previous: Initialization
Contents
Index
Stefan Bilbao
2006-11-15
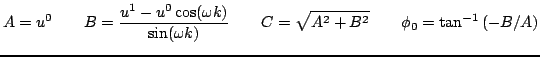
![]() , then the two roots of (
, then the two roots of (![]() ) will be real, and one will be of magnitude greater than unity. Thus solution (3.24) will clearly grow exponentially. If
) will be real, and one will be of magnitude greater than unity. Thus solution (3.24) will clearly grow exponentially. If
![]() , then the two roots of (3.23) coincide, at
, then the two roots of (3.23) coincide, at
![]() . In this case, the solution (3.24) does not hold, and there will be a term which grows linearly. In neither of the above cases does the solution behave in accordance with (3.3), and its size cannot be bounded in terms of initial conditions alone. Such growth is called numerically unstable (and in the latter case marginally unstable), and condition (3.25) serves as a stability condition.
. In this case, the solution (3.24) does not hold, and there will be a term which grows linearly. In neither of the above cases does the solution behave in accordance with (3.3), and its size cannot be bounded in terms of initial conditions alone. Such growth is called numerically unstable (and in the latter case marginally unstable), and condition (3.25) serves as a stability condition.
![]() and oscillator frequency
and oscillator frequency
![]() as
as