




Next: Energy
Up: The Simple Harmonic Oscillator
Previous: The Simple Harmonic Oscillator
Contents
Index
Sinusoidal Solution
It is well-known that the solution to (3.1), if 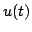 is constrained to be real-valued, and if
is constrained to be real-valued, and if
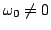 , has the form
, has the form
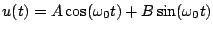 |
(3.3) |
where clearly, one must have
 |
(3.4) |
Another way of writing (3.3) is as
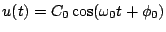 |
(3.5) |
where
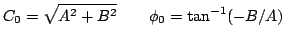 |
(3.6) |
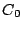 is the amplitude of the sinusoid, and
is the amplitude of the sinusoid, and 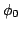 is the initial phase.
is the initial phase.
From the sinusoidal form (3.5) above, it is easy enough to deduce that
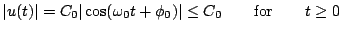 |
(3.7) |
which serves as a convenient bound on the size of the solution for all 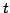 , purely in terms of the initial conditions and the system parameter
, purely in terms of the initial conditions and the system parameter
 . Such bounds, in a numerical sound synthesis setting, are extremely useful, especially if a signal such as
. Such bounds, in a numerical sound synthesis setting, are extremely useful, especially if a signal such as 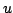 is to be represented in a limited precision audio format. Note however, that the bound above is obtained only through a priori knowledge of the form of the solution itself (i.e., it is a sinusoid). As will be shown in the next section, it is not really necessary to make such an assumption.
is to be represented in a limited precision audio format. Note however, that the bound above is obtained only through a priori knowledge of the form of the solution itself (i.e., it is a sinusoid). As will be shown in the next section, it is not really necessary to make such an assumption.
The use of sinusoidal, or more generally complex exponential solutions to a given system in order to derive bounds on the size of the solution was developed, in the discrete setting, into a framework for determining numerical stability of a simulation algorithm, also known as von Neumann analysis [210,102]. Much more will be said about this from Chapter 5 onwards.





Next: Energy
Up: The Simple Harmonic Oscillator
Previous: The Simple Harmonic Oscillator
Contents
Index
Stefan Bilbao
2006-11-15