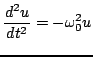 |
(3.1) |
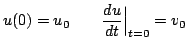 |
(3.2) |
Equation (3.1) above may be arrived at in a variety of different contexts. In mechanics and acoustics, the canonical example is that of the mass/spring system, illustrated in Figure 3.1(a). A mass ![]() is connected, via a linear spring of spring constant
is connected, via a linear spring of spring constant ![]() to a rigid support, and
to a rigid support, and ![]() represents the variation of the displacement of the mass about an equilibrium distance. Under these conditions, and if initial conditions such as
represents the variation of the displacement of the mass about an equilibrium distance. Under these conditions, and if initial conditions such as ![]() and
and ![]() above are given,
above are given, ![]() satisfies (3.1) with
satisfies (3.1) with
![]() . The oscillator also appears naturally in electrical circuit theory, as illustrated in Figure 3.1(b)--here,
. The oscillator also appears naturally in electrical circuit theory, as illustrated in Figure 3.1(b)--here, ![]() represents the voltage across a linear capacitor, of capacitance
represents the voltage across a linear capacitor, of capacitance ![]() in series with an linear inductor of inductance
in series with an linear inductor of inductance ![]() . Again, if appropriate initial conditions are supplied, the voltage will evolve according to (3.1), with
. Again, if appropriate initial conditions are supplied, the voltage will evolve according to (3.1), with
![]() . Though electrical circuit theory would appear to be a poor match for problems involving musical instrument modelling, and in fact will not appear further in this book, it is worth keeping in mind that scattering methods such as digital waveguides [209] and wave digital filters [81], which are heavily used in physical modelling sound synthesis, were all first developed in the context of electrical circuit theory. There is also, of course, a long tradition in acoustics of modeling lumped systems in terms of equivalent circuit elements, primarily for simplicity of representation.
. Though electrical circuit theory would appear to be a poor match for problems involving musical instrument modelling, and in fact will not appear further in this book, it is worth keeping in mind that scattering methods such as digital waveguides [209] and wave digital filters [81], which are heavily used in physical modelling sound synthesis, were all first developed in the context of electrical circuit theory. There is also, of course, a long tradition in acoustics of modeling lumped systems in terms of equivalent circuit elements, primarily for simplicity of representation.
 |