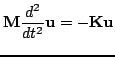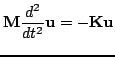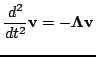Coupled Systems of Oscillators

Coupled second order ODE systems appear frequently in finite element analysis, and, in musical sound synthesis, directly as descriptions of the dynamics of lumped networks, as described in §1.2.1; what remains, after spatial discretization of an LTI distributed system, is a system of the form:

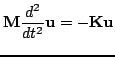$${\bf M}\frac{d^2}{dt^2}{\bf u}=-{\bf K}{\bf u}$$ (3.16)

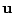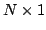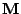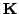where here, ${\bf u}$ is an $N\times 1$ column vector, and ${\bf M}$ and ${\bf K}$ are known as, respectively, the 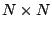$N\times N$ mass and stiffness matrices, which are constants. If the product 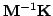${\bf M}^{-1}{\bf K}$ exists and is diagonalizable, with 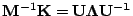${\bf M}^{-1}{\bf K}={\bf U\Lambda U^{-1}}$, then the system may be immediately decoupled as

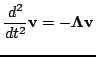$$\frac{d^2}{dt^2}{\bf v}=-{\bf\Lambda}{\bf v}$$ (3.17)

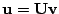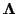where ${\bf u}={\bf U v}$, and ${\bf\Lambda}$ is the diagonal matrix containing the eigenvalues of 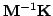${\bf M}^{-1}{\bf K}$. In most cases of interest, 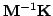${\bf M}^{-1}{\bf K}$ will be symmetric and positive definite.

Lumped network approaches to sound synthesis, mentioned in §1.2.1, are built, essentially, around such coupled oscillator systems. Some simple examples will appear later in §3.4.