A Simple Scheme

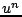The simplest possible finite difference scheme for the simple harmonic oscillator (3.1) is obtained by introducing a time step $k$, a time series $u^n$ intended to approximate the solution at time 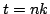$t=nk$, and by replacing the second time derivative by a second time difference, as defined in (2.4). One has, in operator form,

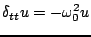$$\delta_{tt}u = -\omega_{0}^2 u$$ (3.18)

Note the compactness of the above representation, and in particular the absence of the time index, which is assumed to be 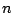$n$ for any occurrence of the variable 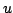$u$. The finite difference scheme (3.18) is a second order accurate approximation to (3.1). A code example in the Matlab programming language is provided in §A.1.