Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In (9.19) of the previous section, we derived that the FBS
reconstruction sum gives
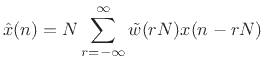 |
(10.20) |
where
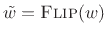 . From this we see that if
. From this we see that if 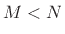 (where
(where  is
the window length and
is
the window length and  is the DFT size), as is normally the case,
then
is the DFT size), as is normally the case,
then 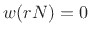 for
for
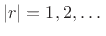 . This is the
Fourier dual
of the ``strong COLA constraint'' for OLA (see
§8.3.2). When it holds, we have
. This is the
Fourier dual
of the ``strong COLA constraint'' for OLA (see
§8.3.2). When it holds, we have
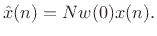 |
(10.21) |
This is simply a gain term, and so we are able to recover the original
signal exactly. (Zero-phase windows are appropriate here.)
If the window length is larger than the number of analysis frequencies
( ), we can still obtain perfect reconstruction provided
), we can still obtain perfect reconstruction provided
![$\displaystyle w(rN) = 0, \hspace{1cm} \vert r\vert=1,2,\dots \qquad\hbox{[$w$\ is Nyquist($N$)]}$](img1616.png) |
(10.22) |
When this holds, we say the window is
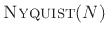 . (This is the dual of
the weak COLA constraint introduced in §8.3.1.) Portnoff windows, discussed
in §9.7, make use of this result; they are
longer than the DFT size and therefore must be used in
time-aliased form [62]. An advantage of
Portnoff windows is that they give reduced overlap among the channel
filter pass-bands. In the limit, a Portnoff window can approach a sinc
function having its zero-crossings at all nonzero multiples of
. (This is the dual of
the weak COLA constraint introduced in §8.3.1.) Portnoff windows, discussed
in §9.7, make use of this result; they are
longer than the DFT size and therefore must be used in
time-aliased form [62]. An advantage of
Portnoff windows is that they give reduced overlap among the channel
filter pass-bands. In the limit, a Portnoff window can approach a sinc
function having its zero-crossings at all nonzero multiples of  samples, thereby yielding an ideal channel filter with bandwidth
samples, thereby yielding an ideal channel filter with bandwidth
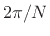 . Figure 9.16 compares example Hamming and Portnoff
windows.
. Figure 9.16 compares example Hamming and Portnoff
windows.
Figure 3.35:
![\includegraphics[width=\twidth]{eps/colawin}](img1618.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
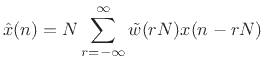
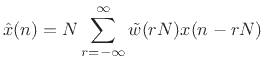
![]() ), we can still obtain perfect reconstruction provided
), we can still obtain perfect reconstruction provided