Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let
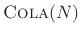 denote constant overlap-add using hop size
denote constant overlap-add using hop size 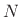 . Then we
have (by the Poisson summation formula Eq.(8.30))
. Then we
have (by the Poisson summation formula Eq.(8.30))
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote constant overlap-add using hop size
denote constant overlap-add using hop size ![]() . Then we
have (by the Poisson summation formula Eq.(8.30))
. Then we
have (by the Poisson summation formula Eq.(8.30))
![\begin{eqnarray*}
w &\in& \hbox{\sc Nyquist}(N) \Leftrightarrow W \in \hbox{\sc Cola}(2\pi/N) \qquad \hbox{(FBS)} \\ [10pt]
w &\in& \hbox{\sc Cola}(R) \Leftrightarrow W \in \hbox{\sc Nyquist}(2\pi/R) \qquad \hbox{(OLA)}
\end{eqnarray*}](img1620.png)