Modulated Gaussian-Windowed Chirp

By the modulation theorem for Fourier transforms,

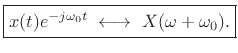$$\zbox {x(t)e^{-j\omega_0t}\;\longleftrightarrow\;X(\omega+\omega_0).}$$ (11.30)

This is proved in §B.6 as the dual of the shift-theorem. It is also evident from inspection of the Fourier transform:

$$\int_{-\infty}^\infty \left[x(t)e^{-j\omega_0 t}\right] e^{-j\omega t} dt \eqsp \int_{-\infty}^\infty x(t)e^{-j(\omega+\omega_0) t} dt \isdefs X(\omega+\omega_0)$$ (11.31)

Applying the modulation theorem to the Gaussian transform pair above yields

$$\zbox {e^{-pt^2} e^{-j\omega_0 t} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} e^{-\frac{(\omega+\omega_0)^2}{4p}},\quad \forall p\in \mathbb{C}: \; \mbox{re}\left\{p\right\}>0.}$$ (11.32)

Thus, we frequency-shift a Gaussian chirp in the same way we frequency-shift any signal--by complex modulation (multiplication by a complex sinusoid at the shift-frequency).