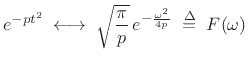 |
(11.33) |
Consider again the Fourier transform of a complex Gaussian in (10.27):
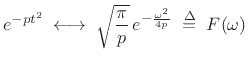 |
(11.33) |
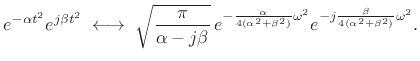 |
(11.34) |
| (11.35) |
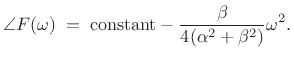 |
(11.36) |
In practice, it is simple to estimate the curvature at a spectral peak using parabolic interpolation:
![\begin{eqnarray*}
c_m &\isdef & \frac{d^2}{d\omega^2} \ln\vert F(\omega)\vert \eqsp - \frac{\alpha}{2(\alpha^2+\beta^2)}\\ [5pt]
c_p &\isdef & \frac{d^2}{d\omega^2} \angle F(\omega) \eqsp - \frac{\beta}{2(\alpha^2+\beta^2)}
\end{eqnarray*}](img1878.png)
We can write

Note that the window ``amplitude-rate'' ![]() is always positive.
The ``chirp rate''
is always positive.
The ``chirp rate'' ![]() may be positive (increasing frequency) or
negative (downgoing chirps). For purposes of chirp-rate estimation,
there is no need to find the true spectral peak because the curvature
is the same for all
may be positive (increasing frequency) or
negative (downgoing chirps). For purposes of chirp-rate estimation,
there is no need to find the true spectral peak because the curvature
is the same for all ![]() . However, curvature estimates are
generally more reliable near spectral peaks, where the signal-to-noise
ratio is typically maximum.
In practice, we can form an estimate of
. However, curvature estimates are
generally more reliable near spectral peaks, where the signal-to-noise
ratio is typically maximum.
In practice, we can form an estimate of ![]() from the known FFT
analysis window (typically ``close to Gaussian'').
from the known FFT
analysis window (typically ``close to Gaussian'').