| (11.25) |
As discussed in §G.8.2, an interesting generalization of sinusoidal modeling is chirplet modeling. A chirplet is defined as a Gaussian-windowed sinusoid, where the sinusoid has a constant amplitude, but its frequency may be linearly ``sweeping.'' This definition arises naturally from the mathematical fact that the Fourier transform of a Gaussian-windowed chirp signal is a complex Gaussian pulse, where a chirp signal is defined as a sinusoid having linearly modulated frequency, i.e., quadratic phase:
| (11.25) |
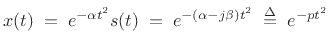 |
(11.26) |
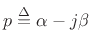 . It is thus clear how naturally
Gaussian amplitude envelopes and linearly frequency-sweeping sinusoids
(chirps) belong together in a unified form called a chirplet.
. It is thus clear how naturally
Gaussian amplitude envelopes and linearly frequency-sweeping sinusoids
(chirps) belong together in a unified form called a chirplet.
The basic chirplet
![]() can be regarded as an
exponential polynomial signal in which the polynomial is of
order 2. Exponential polynomials of higher order have also been
explored [89,90,91].
(See also §G.8.2.)
can be regarded as an
exponential polynomial signal in which the polynomial is of
order 2. Exponential polynomials of higher order have also been
explored [89,90,91].
(See also §G.8.2.)