Cross-Product Magnitude

It is a straightforward exercise to show that the cross-product magnitude is equal to the product of the vector lengths times the sine of the angle between them:^B.21

$$\left\Vert\,\underline{x}\times \underline{y}\,\right\Vert \eqsp \left\Vert\,\underline{x}\,\right\Vert\cdot\left\Vert\,\underline{y}\,\right\Vert \cdot \vert\sin(\theta)\vert \protect$$ (B.16)

where

$$\sin(\theta)\eqsp \sqrt{1-\cos^2(\theta)}$$

with

$$\cos(\theta) \isdefs \frac{\left<\underline{x},\underline{y}\right>}{\left\Vert\,\underline{x}\,\right\Vert\cdot\left\Vert\,\underline{y}\,\right\Vert}. \,\mathrel{\mathop=}\, \frac{x_1y_1+x_2y_2+x_3y_3}{\sqrt{x_1^2+x_2^2+x_3^2}\cdot\sqrt{y_1^2+y_2^2+y_3^2}}$$

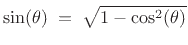
(Recall that the vector cosine of the angle between two vectors is given by their inner product divided by the product of their norms [454].)

To derive Eq.(B.16), let's begin with the cross-product in matrix form as $\underline{x}\times\underline{y}= \mathbf{X}\underline{y}$ using the first matrix form in the third line of the cross-product definition in Eq.(B.15) above. Then

$$\begin{eqnarray*} (\underline{x}\times\underline{y})^2 &=& \underline{y}^T\mathbf{X}^T\mathbf{X}\underline{y} \eqsp \underline{y}^T\left( \vert\vert\,\underline{x}\,\vert\vert ^2\cdot\mathbf{E}- \underline{x}\underline{x}^T\right)\underline{y} \eqsp \underline{y}^T \vert\vert\,\underline{x}\,\vert\vert ^2\left(\mathbf{E}- {\cal P}_{\underline{x}}\right)\underline{y}\\ [5pt] &\isdef & \vert\vert\,\underline{x}\,\vert\vert ^2\underline{y}^T{\cal P}_{\underline{x}^{\tiny\perp}}\underline{y}, \eqsp \vert\vert\,\underline{x}\,\vert\vert ^2\underline{y}^T{\cal P}^T_{\underline{x}^{\tiny\perp}}{\cal P}_{\underline{x}^{\tiny\perp}}\underline{y}, \isdefs \vert\vert\,\underline{x}\,\vert\vert ^2\underline{y}^T_{\underline{x}^{\tiny\perp}}\underline{y}_{\underline{x}^{\tiny\perp}} \end{eqnarray*}$$

where $\mathbf{E}=[\underline{e}_1,\underline{e}_2,\underline{e}_3]$ denotes the identity matrix in $\mathbb{R}^3$ , ${\cal P}_{\underline{x}}$ denotes the orthogonal-projection matrix onto $\underline {x}$ [454], ${\cal P}_{\underline{x}^{\tiny\perp}}$ denotes the projection matrix onto the orthogonal complement of $\underline {x}$ , $\underline{y}_{\underline{x}^{\tiny\perp}}$ denotes the component of $\underline{y}$ orthogonal to $\underline {x}$ , and we used the fact that orthogonal projection matrices ${\cal P}$ are idempotent (i.e., ${\cal P}^2 ={\cal P}$ ) and symmetric (when real, as we have here) when we replaced ${\cal P}_{\underline{x}^{\tiny\perp}}$ by ${\cal P}^T_{\underline{x}^{\tiny\perp}}{\cal P}_{\underline{x}^{\tiny\perp}}$ above. Finally, note that the length of $\underline{y}_{\underline{x}^{\tiny\perp}}$ is $\vert\vert\,\underline{y}\,\vert\vert \cdot\vert\sin(\theta)\vert$ , where $\theta$ is the angle between the 1D subspaces spanned by $\underline {x}$ and $\underline{y}$ in the plane including both vectors. Thus,

$$(\underline{x}\times\underline{y})^2 \eqsp \vert\vert\,\underline{x}\,\vert\vert ^2\underline{y}^T_{\underline{x}^{\tiny\perp}}\underline{y}_{\underline{x}^{\tiny\perp}} \eqsp \vert\vert\,\underline{x}\,\vert\vert ^2 \vert\vert\,\underline{y}_{\underline{x}^{\tiny\perp}}\,\vert\vert ^2 \eqsp \vert\vert\,\underline{x}\,\vert\vert ^2 \vert\vert\,\underline{y}\,\vert\vert ^2\sin^2(\theta),$$

which establishes the desired result:

$$\left\Vert\,\underline{x}\times\underline{y}\,\right\Vert = \vert\vert\,\underline{x}\,\vert\vert \cdot \vert\vert\,\underline{y}\,\vert\vert \cdot\vert\sin(\theta)\vert$$

Moreover, this proof gives an appealing geometric interpretation of the vector cross-product $\underline{x}\times\underline{y}$ as having magnitude given by the product of $\vert\vert\,\underline{x}\,\vert\vert$ times the norm of the difference between $\underline {x}$ and the orthogonal projection of $\underline {x}$ onto $\underline{y}$ ( $\vert\vert\,\underline{x}\times\underline{y}\,\vert\vert = \vert\vert\,\underline{x}\,\vert\vert \cdot \vert\vert\,\underline{x}-{\cal P}_{\underline{y}}(\underline{x})\,\vert\vert$ ) or vice versa ( $\vert\vert\,\underline{x}\times\underline{y}\,\vert\vert = \vert\vert\,\underline{y}\,\vert\vert \cdot \vert\vert\,\underline{y}-{\cal P}_{\underline{x}}(\underline{y})\,\vert\vert$ ). In this geometric picture it is clear that the cross-product magnitude is maximized when the vectors are orthogonal, and it is zero when the vectors are collinear. It is ``length times orthogonal length.''

The direction of the cross-product vector is then taken to be orthogonal to both $\underline {x}$ and $\underline{y}$ according to the right-hand rule. This orthogonality can be checked by verifying that $\mathbf{X}\underline{x}=\mathbf{Y}\underline{y}=\underline{0}$ . The right-hand-rule parity can be checked by rotating the space so that $\underline{x}'=[ \vert\vert\,\underline{x}\,\vert\vert ,0,0]^T$ and $\underline{y}'=[ \vert\vert\,\underline{y}\,\vert\vert \cos(\theta), \vert\vert\,\underline{y}\,\vert\vert \sin(\theta),0]^T$ in which case $\underline{x}'\times\underline{y}' = \vert\vert\,\underline{x}\,\vert\vert [0,0, \vert\vert\,\underline{y}\,\vert\vert \sin(\theta)]^T = \vert\vert\,\underline{x}\,\vert\vert \vert\vert\,\underline{y}\,\vert\vert \sin(\theta)\underline{e}_3$ . Thus, the cross product points ``up'' relative to the $(\underline{x},\underline{y})$ plane for $\theta \in(0,\pi)$ and ``down'' for $\theta\in(0,-\pi)$ .