Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In Eq.(B.14) above, the mass moment of inertia was expressed
in terms of orthogonal projection as
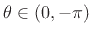 , where
, where
 . In terms of the vector cross
product, we can now express it as
. In terms of the vector cross
product, we can now express it as
where
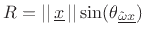 is the distance from the rotation
axis out to the point
is the distance from the rotation
axis out to the point
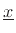 (which equals the length of the vector
(which equals the length of the vector
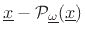 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , where
, where
![]() . In terms of the vector cross
product, we can now express it as
. In terms of the vector cross
product, we can now express it as