In previous work, time-domain adaptors (digital filters) converting
between K variables and W variables have been devised
[224]. In this section, an alternative approach is
proposed. Mapping Eq.(E.7) gives us an immediate conversion from W
to K state variables, so all we need now is the inverse map for any
time ![]() . This is complicated by the fact that non-local spatial
dependencies can go indefinitely in one direction along the string, as
we will see below. We will proceed by first writing down the
conversion from W to K variables in matrix form, which is easy to do,
and then invert that matrix. For simplicity, we will consider the
case of an infinitely long string.
. This is complicated by the fact that non-local spatial
dependencies can go indefinitely in one direction along the string, as
we will see below. We will proceed by first writing down the
conversion from W to K variables in matrix form, which is easy to do,
and then invert that matrix. For simplicity, we will consider the
case of an infinitely long string.
To initialize a K variable simulation for starting at time ![]() , we
need initial spatial samples at all positions
, we
need initial spatial samples at all positions ![]() for two successive
times
for two successive
times ![]() and
and ![]() . From this state specification, the FDTD scheme
Eq.(E.3) can compute
. From this state specification, the FDTD scheme
Eq.(E.3) can compute ![]() for all
for all ![]() , and so on for
increasing
, and so on for
increasing ![]() . In the DW model, all state variables are defined as
belonging to the same time
. In the DW model, all state variables are defined as
belonging to the same time ![]() , as shown in Fig.E.2.
, as shown in Fig.E.2.
From Eq.(E.6), and referring to the notation defined in
Fig.E.2, we may write the conversion from W to K variables
as
Figure E.3 shows the so-called ``stencil'' of the FDTD scheme.
The larger circles indicate the state at time ![]() which can be used to
compute the state at time
which can be used to
compute the state at time ![]() . The filled and unfilled circles
indicate membership in one of two interleaved grids [55]. To
see why there are two interleaved grids, note that when
. The filled and unfilled circles
indicate membership in one of two interleaved grids [55]. To
see why there are two interleaved grids, note that when ![]() is even,
the update for
is even,
the update for ![]() depends only on odd
depends only on odd ![]() from time
from time ![]() and even
and even
![]() from time
from time ![]() . Since the two W components of
. Since the two W components of ![]() are converted to
two W components at time
are converted to
two W components at time ![]() in Eq.(E.8), we have that the update for
in Eq.(E.8), we have that the update for
![]() depends only on W components from time
depends only on W components from time ![]() and positions
and positions
![]() .
Moving to the next position update, for
.
Moving to the next position update, for
![]() , the state used is
independent of that used for
, the state used is
independent of that used for ![]() , and the W components used are
from positions
, and the W components used are
from positions ![]() and
and ![]() . As a result of these observations, we
see that we may write the state-variable transformation separately for
even and odd
. As a result of these observations, we
see that we may write the state-variable transformation separately for
even and odd ![]() , e.g.,
, e.g.,
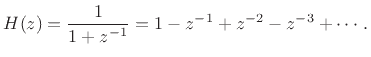
Therefore, we may easily write down the inverted transformation: