Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As discussed in §C.2, we may use centered finite
difference approximations (FDA) for the
second-order partial derivatives in the wave equation to obtain a
finite difference scheme for numerically integrating the ideal
wave equation [484,314]:
where 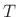 is the time sampling interval, and
is the time sampling interval, and  is a spatial
sampling interval.
is a spatial
sampling interval.
Substituting the FDA into the wave equation, choosing 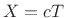 ,
where
,
where
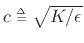 is sound speed (normalized to
is sound speed (normalized to 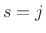 below), and sampling at times
below), and sampling at times  and positions
and positions 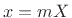 , we
obtain the following explicit finite difference scheme for the string
displacement:
, we
obtain the following explicit finite difference scheme for the string
displacement:
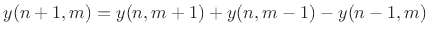 |
(E.3) |
where the sampling intervals 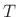 and
and  have been normalized to
1. To initialize the recursion at time
have been normalized to
1. To initialize the recursion at time 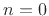 , past values are needed
for all
, past values are needed
for all  (all points along the string) at time instants
(all points along the string) at time instants 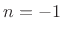 and
and
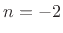 . Then the string position may be computed for all
. Then the string position may be computed for all  by
Eq.(E.3) for
by
Eq.(E.3) for
 . This has been called the
FDTD or leapfrog finite difference scheme [128].
. This has been called the
FDTD or leapfrog finite difference scheme [128].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
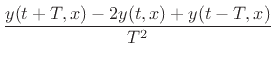
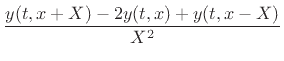
![]() ,
where
,
where
![]() is sound speed (normalized to
is sound speed (normalized to ![]() below), and sampling at times
below), and sampling at times ![]() and positions
and positions ![]() , we
obtain the following explicit finite difference scheme for the string
displacement:
, we
obtain the following explicit finite difference scheme for the string
displacement: