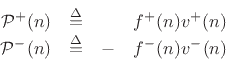Power Waves

Basic courses in physics teach us that power is work per unit time, and work is a measure of energy which is typically defined as force times distance. Therefore, power is in physical units of force times distance per unit time, or force times velocity. It therefore should come as no surprise that traveling power waves are defined for strings as follows:

$$\begin{array}{rcrl} {\cal P}^{+}(n) &\isdef &&f^{{+}}(n)v^{+}(n) \\ {\cal P}^{-}(n) &\isdef &-&f^{{-}}(n)v^{-}(n) \end{array}$$

From the Ohm's-law relations $f^{{+}}= Rv^{+}$ and $f^{{-}}=-Rv^{-}$ , we also have

$$\begin{eqnarray*} {\cal P}^{+}(n)&=&R[v^{+}(n)]^2 \eqsp [f^{{+}}(n)]^2/R, \\ {\cal P}^{-}(n)&=&R[v^{-}(n)]^2 \eqsp [f^{{-}}(n)]^2/R. \end{eqnarray*}$$

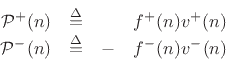Thus, both the left- and right-going components are nonnegative. The sum of the traveling powers at a point gives the total power at that point in the waveguide:

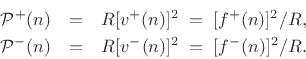$${\cal P}(t_n,x_m) \isdefs {\cal P}^{+}(n-m) + {\cal P}^{-}(n+m)$$ (C.49)

If we had left out the minus sign in the definition of left-going power waves, the sum would instead be a net power flow.

Power waves are important because they correspond to the actual ability of the wave to do work on the outside world, such as on a violin bridge at the end of a string. Because energy is conserved in closed systems, power waves sometimes give a simpler, more fundamental view of wave phenomena, such as in conical acoustic tubes. Also, implementing nonlinear operations such as rounding and saturation in such a way that signal power is not increased, gives suppression of limit cycles and overflow oscillations [436], as discussed in the section on signal scattering.

For example, consider a waveguide having a wave impedance which increases smoothly to the right. A converging cone provides a practical example in the acoustic tube realm. Then since the energy in a traveling wave must be in the wave unless it has been transduced elsewhere, we expect ${\cal P}^{+}$ to propagate unchanged along the waveguide. However, since the wave impedance is increasing, it must be true that force is increasing and velocity is decreasing according to ${\cal P}^{+}= R(v^{+})^2 = (f^{{+}})^2/R$ . Looking only at force or velocity might give us the mistaken impression that the wave is getting stronger (looking at force) or weaker (looking at velocity), when really it was simply sailing along as a fixed amount of energy. This is an example of a transformer action in which force is converted into velocity or vice versa. It is well known that a conical tube acts as if it's open on both ends even though we can plainly see that it is closed on one end. A tempting explanation is that the cone acts as a transformer which exchanges pressure and velocity between the endpoints of the tube, so that a closed end on one side is equivalent to an open end on the other. However, this view is oversimplified because, while spherical pressure waves travel nondispersively in cones, velocity propagation is dispersive [22,50].