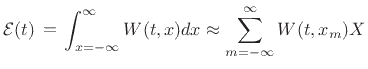Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Energy Density Waves
The vibrational energy per unit length along the string, or wave
energy density [320] is given by the sum of potential and
kinetic energy densities:
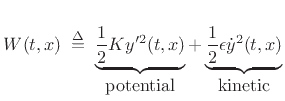 |
(C.50) |
Sampling across time and space, and substituting traveling wave components,
one can show in a few lines of algebra that the sampled wave energy
density is given by
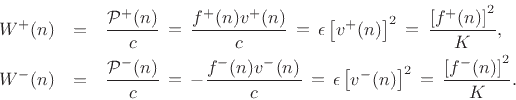 |
(C.51) |
where
Thus, traveling power waves (energy per unit time)
can be converted to energy density waves (energy per unit length) by
simply dividing by 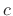 , the speed of propagation. Quite naturally, the
total wave energy in the string
is given by the integral along the string of the energy density:
, the speed of propagation. Quite naturally, the
total wave energy in the string
is given by the integral along the string of the energy density:
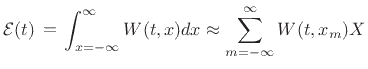 |
(C.52) |
In practice, of course, the string length is finite, and the limits
of integration are from the  coordinate of the left endpoint to
that of the right endpoint, e.g., 0
to
coordinate of the left endpoint to
that of the right endpoint, e.g., 0
to  .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
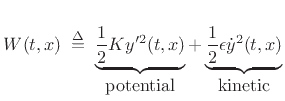
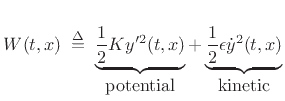
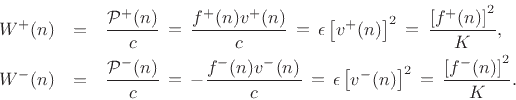
![\begin{eqnarray*}
W^{+}(n) &=& \frac{{\cal P}^{+}(n)}{c} \,\mathrel{\mathop=}\,\frac{f^{{+}}(n)v^{+}(n)}{c}
\,\mathrel{\mathop=}\,\epsilon \left[v^{+}(n)\right]^2 \,\mathrel{\mathop=}\,\frac{\left[f^{{+}}(n)\right]^2}{K}, \\
W^{-}(n) &=& \frac{{\cal P}^{-}(n)}{c} \,\mathrel{\mathop=}\,-\frac{f^{{-}}(n)v^{-}(n)}{c}
\,\mathrel{\mathop=}\,\epsilon \left[v^{-}(n)\right]^2 \,\mathrel{\mathop=}\,\frac{\left[f^{{-}}(n)\right]^2}{K}.
\end{eqnarray*}](img3511.png)
![]() , the speed of propagation. Quite naturally, the
total wave energy in the string
is given by the integral along the string of the energy density:
, the speed of propagation. Quite naturally, the
total wave energy in the string
is given by the integral along the string of the energy density: