State Conversions

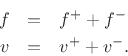
In §C.3.6, an arbitrary string state was converted to traveling displacement-wave components to show that the traveling-wave representation is complete, i.e., that any physical string state can be expressed as a pair of traveling-wave components. In this section, we revisit this topic using force and velocity waves.

By definition of the traveling-wave decomposition, we have

$$\begin{eqnarray*} f&=&f^{{+}}+f^{{-}}\\ v&=&v^{+}+v^{-}. \end{eqnarray*}$$

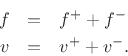
Using Eq.(C.46), we can eliminate $v^{+}=f^{{+}}/R$ and $v^{-}=-f^{{+}}/R$ , giving, in matrix form,

$$\left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\begin{array}{cc} 1 & 1 \\ [2pt] \frac{1}{R} & -\frac{1}{R} \end{array}\right] \left[\begin{array}{c} f^{{+}} \\ [2pt] f^{{-}} \end{array}\right].$$

Thus, the string state (in terms of force and velocity) is expressed as a linear transformation of the traveling force-wave components. Using the Ohm's law relations to eliminate instead $f^{{+}}= Rv^{+}$ and $f^{{-}}=-Rv^{-}$ , we obtain

$$\left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\begin{array}{cc} R & -R \\ [2pt] 1 & 1 \end{array}\right]\left[\begin{array}{c} v^{+} \\ [2pt] v^{-} \end{array}\right].$$

To convert an arbitrary initial string state $(f,v)$ to either a traveling force-wave or velocity-wave simulation, we simply must be able to invert the appropriate two-by-two matrix above. That is, the matrix must be nonsingular. Requiring both determinants to be nonzero yields the condition

$$0 < R < \infty.$$

That is, the wave impedance must be a positive, finite number. This restriction makes good physical sense because one cannot propagate a finite-energy wave in either a zero or infinite wave impedance.

Carrying out the inversion to obtain force waves $(f^{{+}},f^{{-}})$ from $(f,v)$ yields

$$\left[\begin{array}{c} f^{{+}} \\ [2pt] f^{{-}} \end{array}\right] = \frac{1}{2}\left[\begin{array}{cc} 1 & R \\ [2pt] 1 & -R \end{array}\right] \left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\begin{array}{c} \frac{f+Rv}{2} \\ [2pt] \frac{f-Rv}{2} \end{array}\right].$$

Similarly, velocity waves $(v^{+},v^{-})$ are prepared from $(f,v)$ according to

$$\left[\begin{array}{c} v^{+} \\ [2pt] v^{-} \end{array}\right] = \frac{1}{2}\left[\begin{array}{cc} \frac{1}{R} & 1 \\ [2pt] -\frac{1}{R} & 1 \end{array}\right] \left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\begin{array}{c} \frac{v+f/R}{2} \\ [2pt] \frac{v-f/R}{2} \end{array}\right].$$