From Eq.(C.75),
we have that the reflectance seen at a continuous-time impedance
![]() is given for force waves by
is given for force waves by
If the impedance ![]() goes to infinity (becomes rigid), then
goes to infinity (becomes rigid), then
![]() approaches
approaches ![]() , a result which agrees with an analysis of
rigid string terminations (p.
, a result which agrees with an analysis of
rigid string terminations (p. ![]() ). Similarly, when the
impedance goes to zero,
). Similarly, when the
impedance goes to zero,
![]() becomes
becomes ![]() , which agrees with
the physics of a string with a free end. In acoustic stringed
instruments, bridges are typically quite rigid, so that
, which agrees with
the physics of a string with a free end. In acoustic stringed
instruments, bridges are typically quite rigid, so that
![]() for all
for all ![]() . If a body resonance is
strongly coupled through the bridge,
. If a body resonance is
strongly coupled through the bridge,
![]() can be
significantly smaller than 1 at the resonant frequency
can be
significantly smaller than 1 at the resonant frequency ![]() .
.
Solving for ![]() in Eq.(C.77), we can characterize every
impedance in terms of its reflectance:
in Eq.(C.77), we can characterize every
impedance in terms of its reflectance:
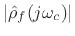
Rewriting Eq.(C.76) in the form
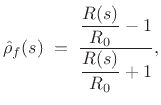
we see that the reflectance is determined by the ratio of the ``new impedance''
In the discrete-time case, which may be related to the continuous-time
case by the bilinear transform (§7.3.2), we have the same basic
relations, but in the ![]() plane:
plane:
 denotes admittance, with
denotes admittance, with
Note that Eq.(C.79) may be obtained from the general formula for
scattering at a loaded waveguide junction for the case of a single
waveguide (![]() ) terminated by a lumped load (§C.12).
) terminated by a lumped load (§C.12).
In the limit as damping goes to zero (all poles of ![]() converge to
the unit circle),
the reflectance
converge to
the unit circle),
the reflectance
![]() becomes a digital allpass filter. Similarly,
becomes a digital allpass filter. Similarly,
![]() becomes a continuous-time allpass filter as the poles of
becomes a continuous-time allpass filter as the poles of
![]() approach the
approach the ![]() axis.
axis.
Recalling that a lossless impedance is called a reactance
(§7.1), we can say that every reactance gives rise to an
allpass reflectance. Thus, for example, waves reflecting off a
mass at the end of a vibrating string will be allpass filtered,
because the driving-point impedance of a mass (![]() ) is a pure
reactance. In particular, the force-wave reflectance of a mass
) is a pure
reactance. In particular, the force-wave reflectance of a mass ![]() terminating an ideal string having wave impedance
terminating an ideal string having wave impedance ![]() is
is
![]() , which is a continuous-time allpass filter having
a pole at
, which is a continuous-time allpass filter having
a pole at ![]() and a zero at
and a zero at ![]() .
.
It is intuitively reasonable that a passive reflection gain cannot
exceed ![]() at any frequency (i.e., the reflectance is a Schur filter,
as defined in Eq.(C.79)). It is also reasonable that lossless
reflection would have a gain of 1 (i.e., it is allpass).
at any frequency (i.e., the reflectance is a Schur filter,
as defined in Eq.(C.79)). It is also reasonable that lossless
reflection would have a gain of 1 (i.e., it is allpass).
Note that reflection filters always have an equal number of poles and zeros, as can be seen from Eq.(C.76) above. This property is preserved by the bilinear transform, so it holds in both the continuous- and discrete-time cases.