Definition. A Schur function
Definition. A Schur function ![]() is defined as a complex function analytic and of modulus not exceeding
unity in
is defined as a complex function analytic and of modulus not exceeding
unity in ![]() .
.
Theorem. The function
Proof.
Suppose ![]() is positive real. Then for
is positive real. Then for ![]() ,
re
,
re![]() re
re![]() is PR. Consequently,
is PR. Consequently, ![]() is minimum phase which implies all roots of
is minimum phase which implies all roots of ![]() lie in the unit circle.
Thus
lie in the unit circle.
Thus ![]() is analytic in
is analytic in ![]() . Also,
. Also,
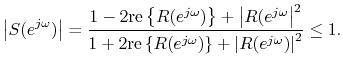
Conversely, suppose ![]() is Schur. Solving Eq.
is Schur. Solving Eq.![]() (5) for
(5) for ![]() gives
gives
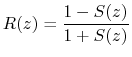
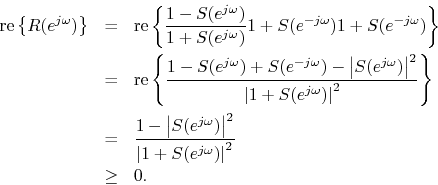
If
![]() is constant, then
is constant, then
![]() is PR. If
is PR. If ![]() is not
constant, then by the maximum principle,
is not
constant, then by the maximum principle, ![]() for
for ![]() . By
Rouche's theorem applied on a circle of radius
. By
Rouche's theorem applied on a circle of radius
![]() ,
,
![]() , on
which
, on
which ![]() , the function
, the function ![]() has the same number of
zeros as the function
has the same number of
zeros as the function ![]() in
in
![]() . Hence,
. Hence, ![]() is
minimum phase which implies
is
minimum phase which implies ![]() is analytic for
is analytic for ![]() . Thus
. Thus
![]() is PR.
is PR.![]()