Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Rigid Terminations
A rigid termination is the simplest case of a string (or tube)
termination. It imposes the constraint that the string (or air) cannot move
at the termination. (We'll look at the more practical case of a yielding
termination in §9.2.1.) If we terminate a length 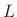 ideal string at
ideal string at
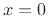 and
and 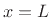 , we then have the ``boundary conditions''
, we then have the ``boundary conditions''
 |
(7.9) |
where ``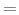 '' means ``identically equal to,'' i.e., equal for all
'' means ``identically equal to,'' i.e., equal for all
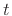 . Let
. Let
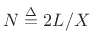 denote the time in samples to propagate
from one end of the string to the other and back, or the total
``string loop'' delay. The loop delay
denote the time in samples to propagate
from one end of the string to the other and back, or the total
``string loop'' delay. The loop delay 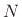 is also equal to twice the
number of spatial samples along the string.
is also equal to twice the
number of spatial samples along the string.
Applying the traveling-wave decomposition from Eq.(6.2), we have
Therefore, solving for the reflected waves gives
A digital simulation diagram for the
rigidly terminated ideal string is shown in Fig.6.3.
A ``virtual pickup'' is shown at the arbitrary location 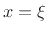 .
.
Figure 6.3:
The rigidly terminated
ideal string, with a displacement output indicated at position
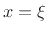 . Rigid terminations reflect traveling displacement, velocity,
or acceleration waves with a sign inversion. Slope or force waves
reflect with no sign inversion.
. Rigid terminations reflect traveling displacement, velocity,
or acceleration waves with a sign inversion. Slope or force waves
reflect with no sign inversion.
![\includegraphics[width=\twidth]{eps/fterminatedstring}](img1362.png) |
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ideal string at
ideal string at
![]() and
and ![]() , we then have the ``boundary conditions''
, we then have the ``boundary conditions''
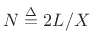 denote the time in samples to propagate
from one end of the string to the other and back, or the total
``string loop'' delay. The loop delay
denote the time in samples to propagate
from one end of the string to the other and back, or the total
``string loop'' delay. The loop delay 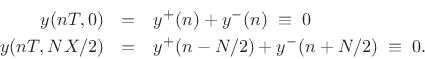
![\includegraphics[width=\twidth]{eps/fterminatedstring}](img1362.png)