Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It can be readily checked (see §C.3 for details)
that the lossless 1D wave equation
(where all terms are defined in Eq.(6.1)) is solved by
any string shape which travels to the left or right with speed
If we denote right-going traveling waves in general by
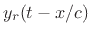 and left-going traveling waves by
and left-going traveling waves by
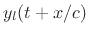 , where
, where 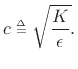 and
and  are arbitrary twice-differentiable functions, then the general class
of solutions to the lossless, one-dimensional, second-order wave
equation can be expressed as
are arbitrary twice-differentiable functions, then the general class
of solutions to the lossless, one-dimensional, second-order wave
equation can be expressed as
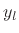 |
(7.2) |
Note that we have
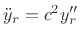 and
and
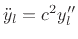 (derived in §C.3.1) showing that the wave
equation is satisfied for all traveling wave shapes
(derived in §C.3.1) showing that the wave
equation is satisfied for all traveling wave shapes 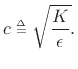 and
and  .
However, the derivation of the wave equation itself assumes the string
slope
.
However, the derivation of the wave equation itself assumes the string
slope
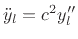 is much less than
is much less than 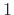 at all times and positions
(see §B.6). An important point to note is that a
function of two variables
at all times and positions
(see §B.6). An important point to note is that a
function of two variables 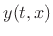 is replaced by two functions of a
single (time) variable. This leads to great reductions in
computational complexity, as we will see. The traveling-wave solution
of the wave equation was first published by d'Alembert in 1747
[100]7.1
is replaced by two functions of a
single (time) variable. This leads to great reductions in
computational complexity, as we will see. The traveling-wave solution
of the wave equation was first published by d'Alembert in 1747
[100]7.1
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
